Excelで構成比を求めることがあります。小さい数Aを大きい数Bで割ると(=A/B)、Aが、B全体の中で何%の割合を占めているかが分かります。いや、分かるはずなんですよ・・・
ところが、割合の計算が苦手な人は、5000円を200円で割ることは理解できても、200円を5000円で割る意味が分かっていません。もはや普通の割り算ではない!と割り切って考えたほうが良いです。電卓で計算したら0.04ですが、この小数の意味が分からなかったら、構成比率を求める意味がありません。
そこで今回は、全体に占める割合、構成比率の求め方とそのパーセンテージの読み方をExcelで出題します。
目次
- 1.大きい数で割る感覚
- 2.構成比率とは何か
- 3.売上数量構成比と売上金額構成比
- 4.構成比率を計算する意味を考えなさい
- 5.構成比率の練習問題
- 6.合計が増えたら構成比率は下がる
- 7.内訳と構成比率から合計を求める
- 8.動画版はこちら(無料)
1.大きい数で割る感覚
上の例では、財布の中に5000円があって200円の買い物をしたと考えます。財布には4800円が残るので「そんなに使っていない」「大半のお金が財布に残っている」という感覚だと思います。これが大きい数で割るという感覚です。
小さい数を大きい数で割ると必ず0~1の小数になります。0に近いほうが全体の中でとても少ないことを表し、1に近いほうが全体の中で多く占めていることを表します。全体が5000円であれば200円はとても少ないので、200/5000は0に近い答えになります。逆に、4800/5000は1に近くなります。

半分より多い、半分より少ないというのを考えると電卓を使わなくても割り算の答えを予想することもできます。例えば、155/355は、半分よりやや少なめなので0.4くらい?という予想ができるはずです。6969/9696は約0.7と予想できます。

この考え方を利用して「一部 / 全体」という表現をすることがあります。例えば、100ページの資料の70ページ目は「70/100」と表現します。10個の荷物のうちの4つ目は「4/10」です。
2.構成比率とは何か
問題
次の図で、各学年の構成比率を求めなさい。
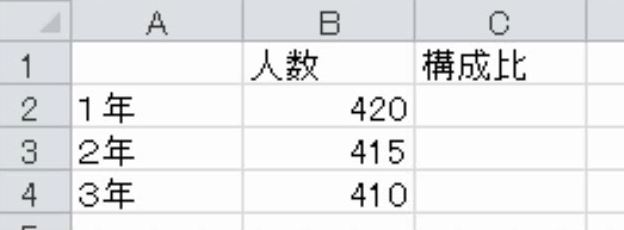
解説
構成比率とは全体に対する割合のことです。全体が100%で、半分が50%です。
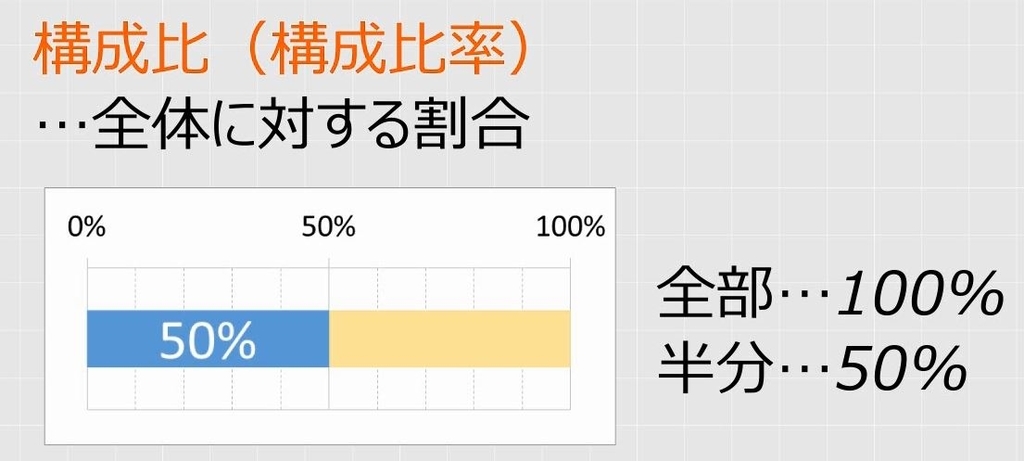
増減の場合とは異なり、増えたり減ったりという意味を持たないので、マイナスになることもなければ、100%を超えることもありません。必ず0~1(0%~100%)になります。
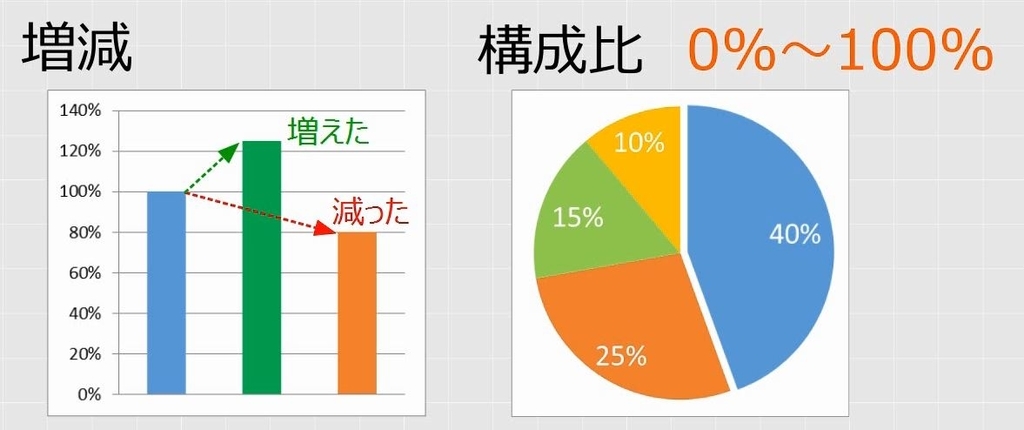
大小関係(包含関係)があって一方が他方に含まれる関係にあります。合計で割ることによって構成比率を出します。

表の中に合計がないときは合計を求めてから考えます。

1245人です。1年生の比率は420/1245です。1200人のうちの400人と考えれば、その比率はだいたい0.3程度ではないかと推測できます(推測できない人はもう一度、上の数直線を見ながら確認してください)。下向きにオートフィルをしますので、合計は絶対参照です(参考:【Excel】絶対参照は表の形とコピーの有無で判断できるように練習せよ )。
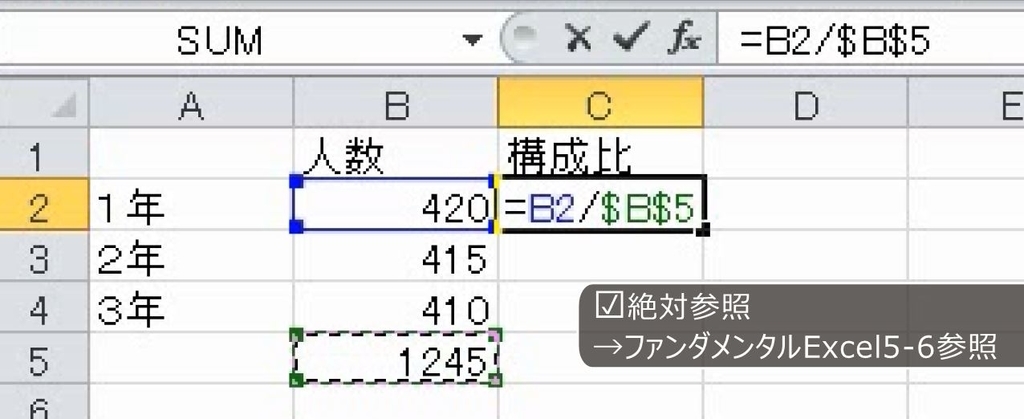
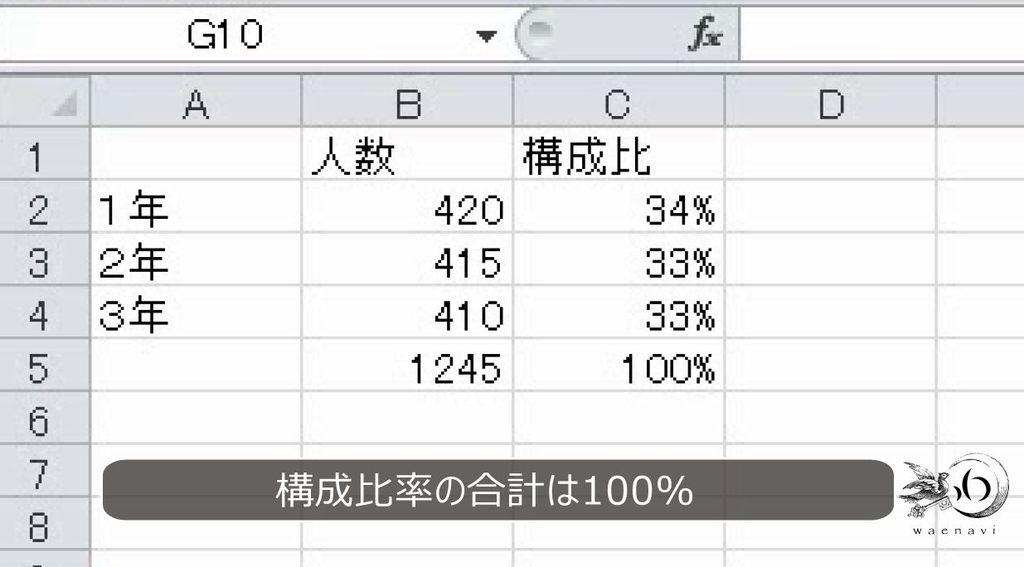
オートフィルをします。これで完成です。原則として構成比率の合計は100%になります。
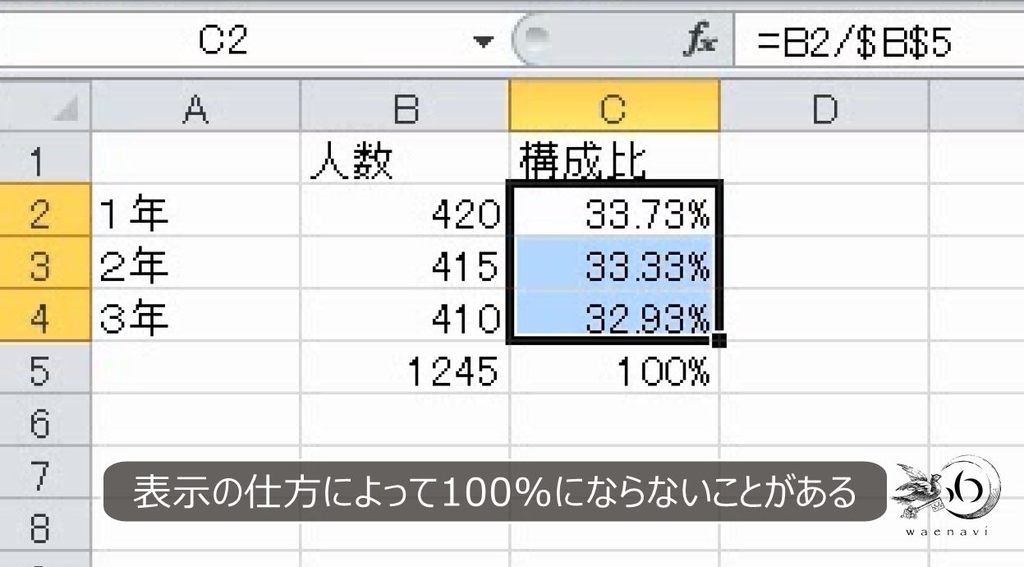
小数第1位もしくは小数第2位まで求めると、合計で100%にはなりません。
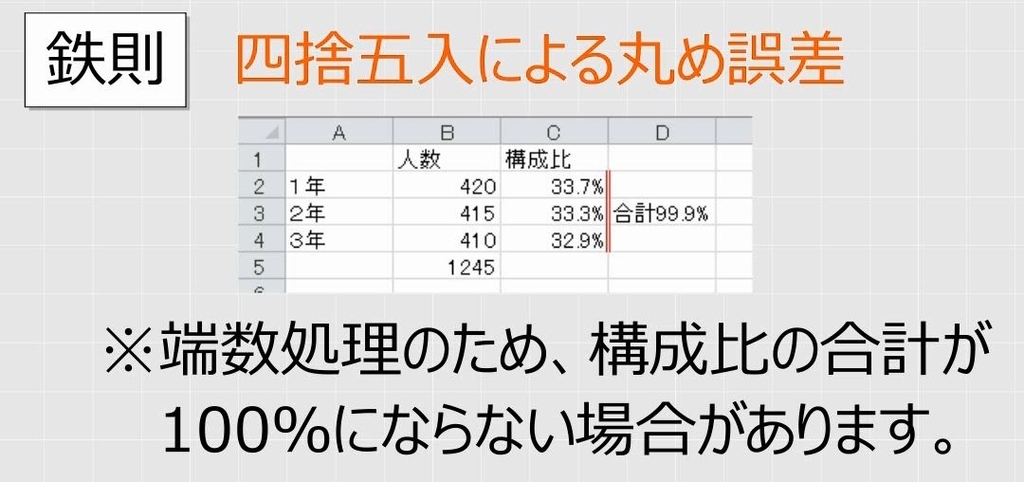
これは、表示形式によって四捨五入しているため、丸め誤差が発生しているからです。構成比率はこのような注意書きが必要です。
3.売上数量構成比と売上金額構成比
問題
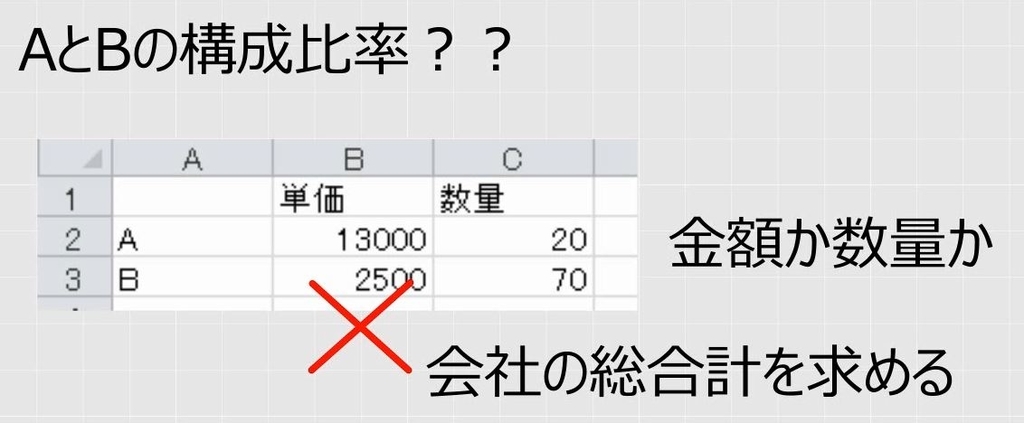
次の図で、2つの商品AとBを売っている会社の場合、AとBの売上数量構成比と金額構成比を求めなさい。

解説
AとBで構成比率を求めるといっても、数量で計算するのか売上金額で計算するのかによって計算式が異なります。数量にしても金額にしても会社の総合計を求める必要があります。単価を足しても意味がありません。
まずはAとB、それぞれの売上金額を求めます。単価x数量です。
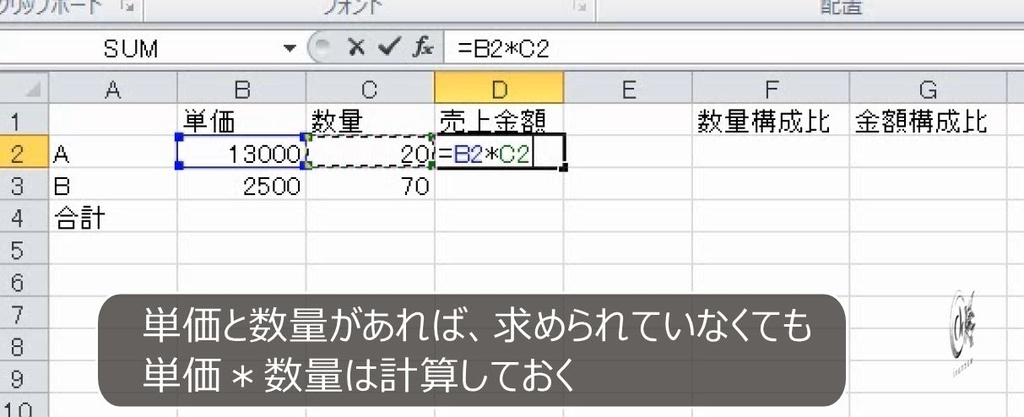
次に構成比率を求めますから、AとBを足して合計を出します。
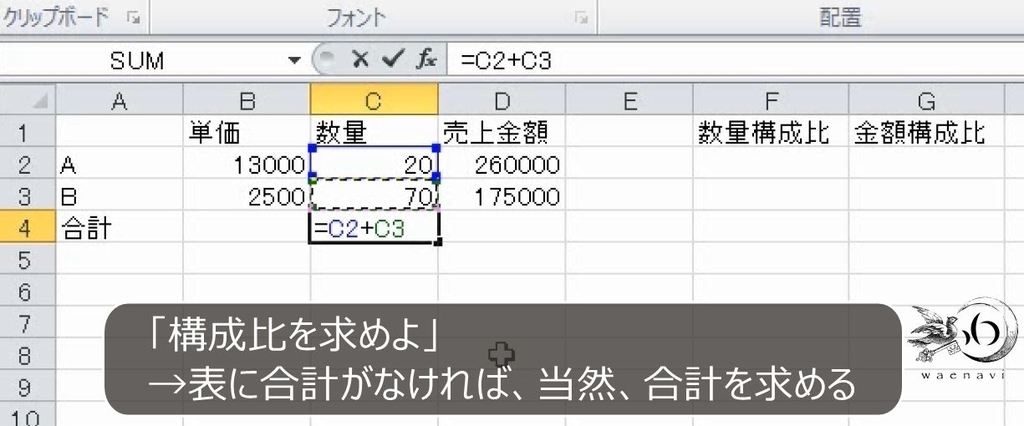
AとBあわせて90個、435000円の売り上げだったことが分かります。数量の構成比は20/90です。縦横にオートフィルすることを考えれば、合計数量は4行目だけ固定する複合参照です(=C2/C$4)。(参考:【Excel複合参照】行固定や列固定のドルマークの意味と練習問題)
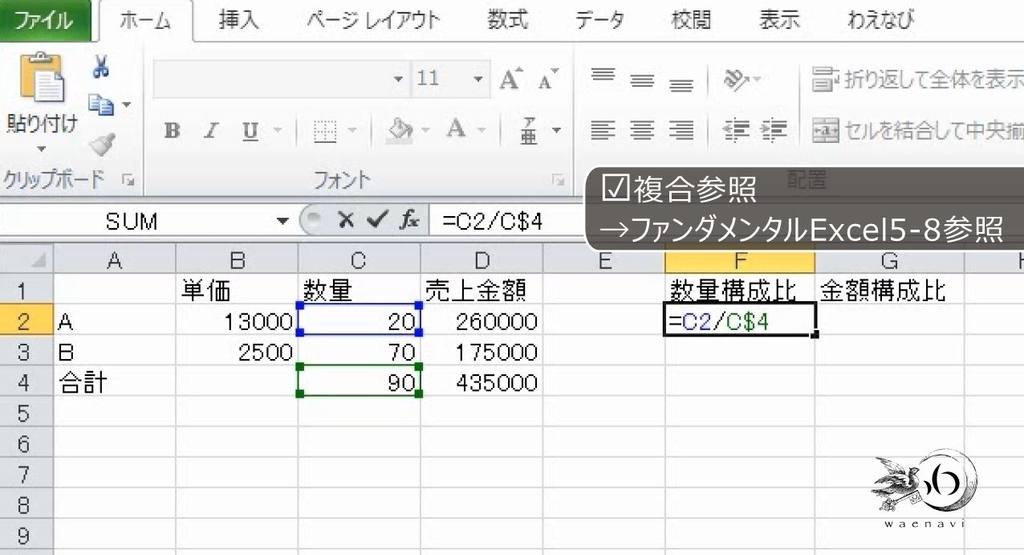
オートフィルをします。これで完成です。数量は2:7の割合でBのほうが多いですが、Aのほうが単価が高いので金額ではAのほうが上回っています。
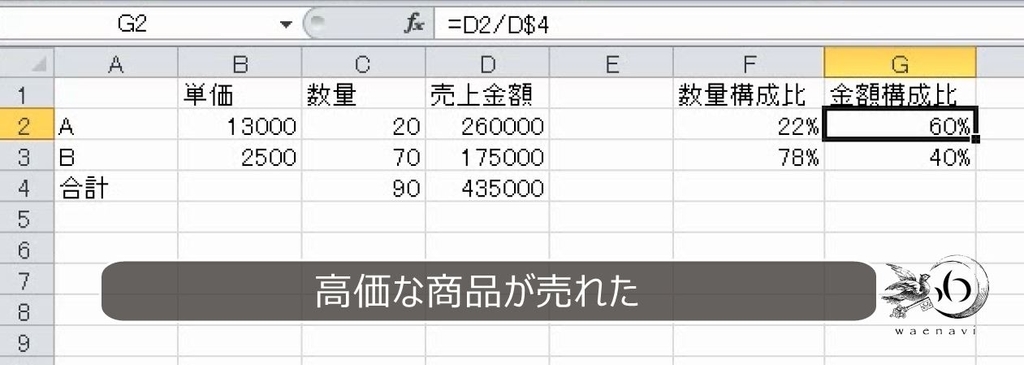
4.構成比率を計算する意味を考えなさい
問題
「表を用いて女子学生構成比を求めよ」との問題を出題したところ、残念ながら、下の(1)~(5)のような誤答があった。それぞれ誤りを指摘しなさい。また、女子学生構成比を正しく求めなさい。

誤答例(1)
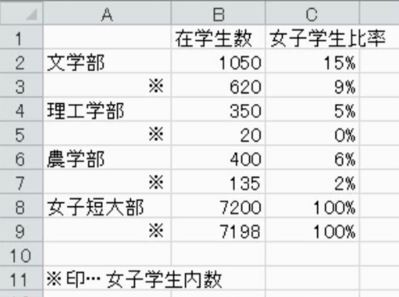
誤答例(2)

誤答例(3)

誤答例(4)
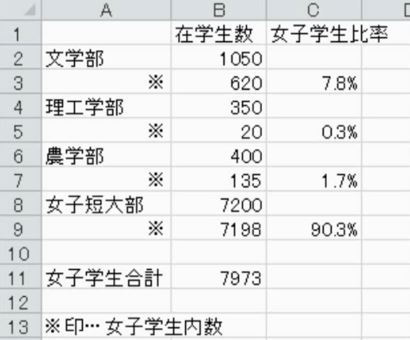
誤答例(5)
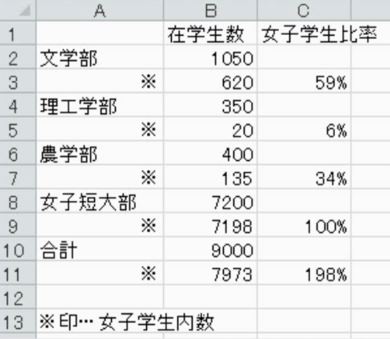
解説
(1)合計がない
1つ目の回答は構成比の意味を全く考えていない例です。合計を出すわけでもなく、性別を考慮したわけでもありません。
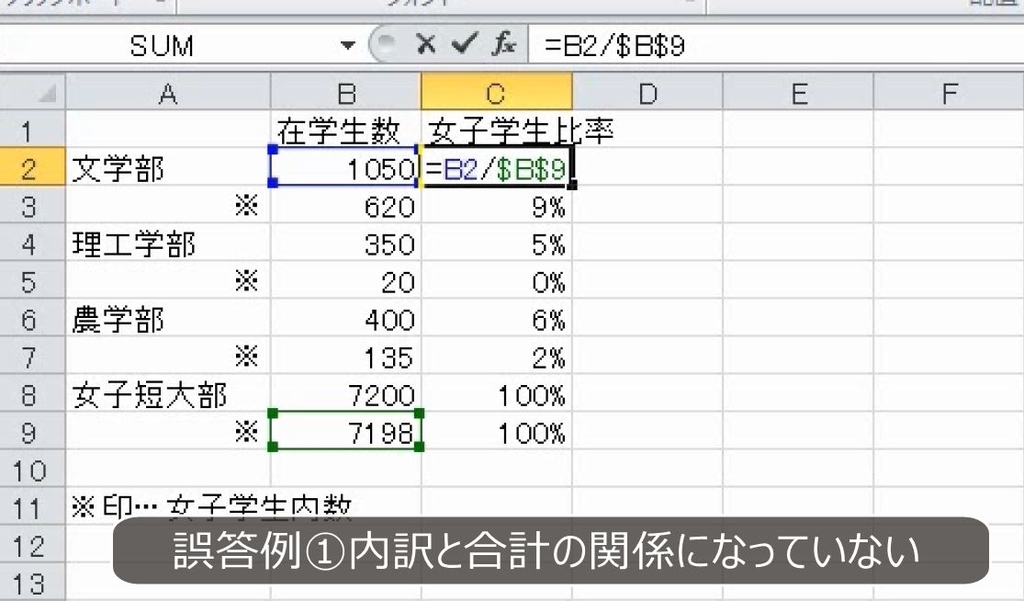
構成比を求めるときに割り算をする2つの数は、必ず一方が他方を含む関係であることが必要です。
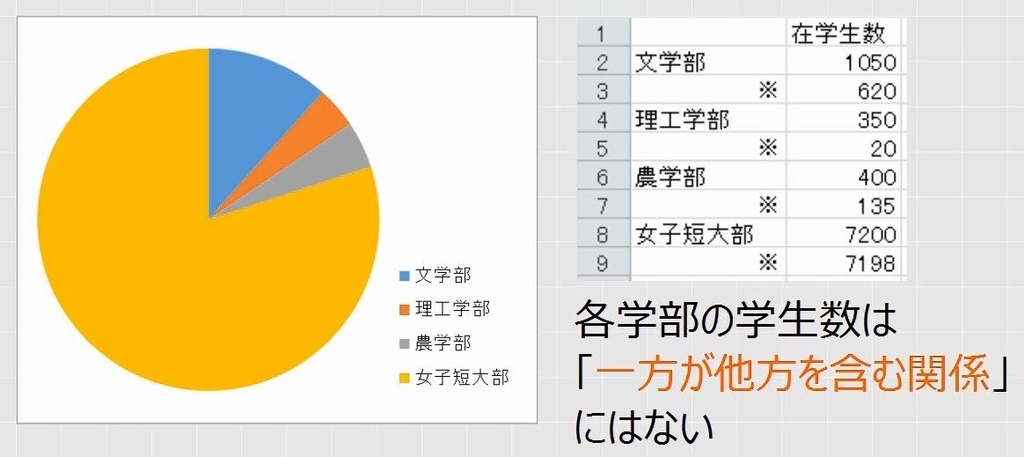
(2)内数(うちすう)を足してはいけない
2つ目の回答は、B列の数値を合計して16973人としています。
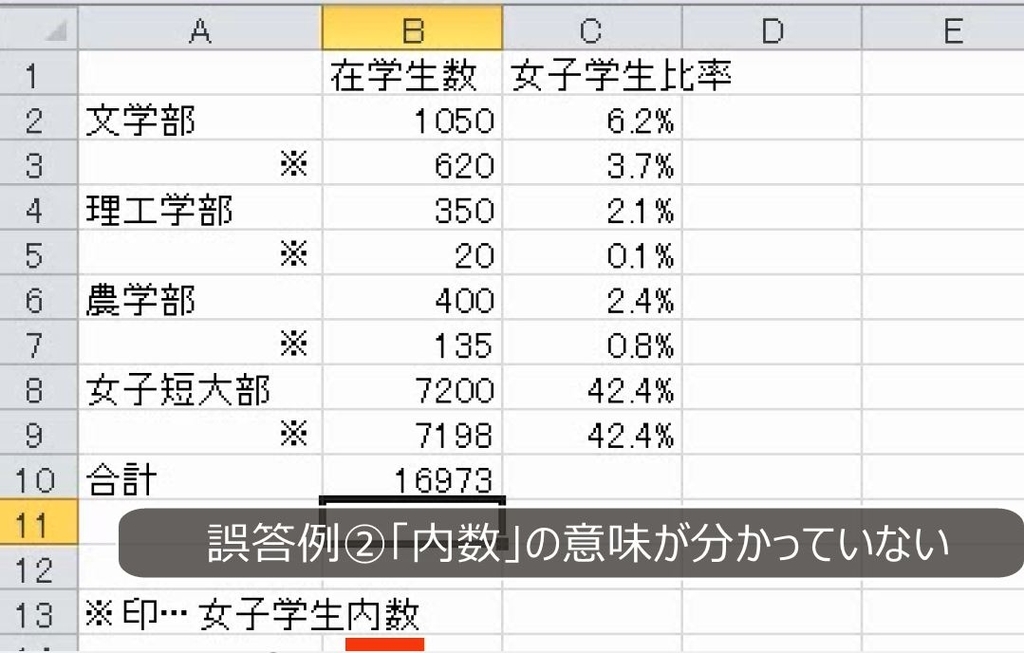
含まれていることを表す数を内数(うちすう)といいます。女子短大部の7200人は男女の合計数であり、そのうち7198人が女子学生であることを表しています。

この学校の4つの学部をすべて足しても、10000人も学生はいません。また、女子短大部の学生が7000人もいるのに比率が42.4%と半分を切っていることも不自然です。
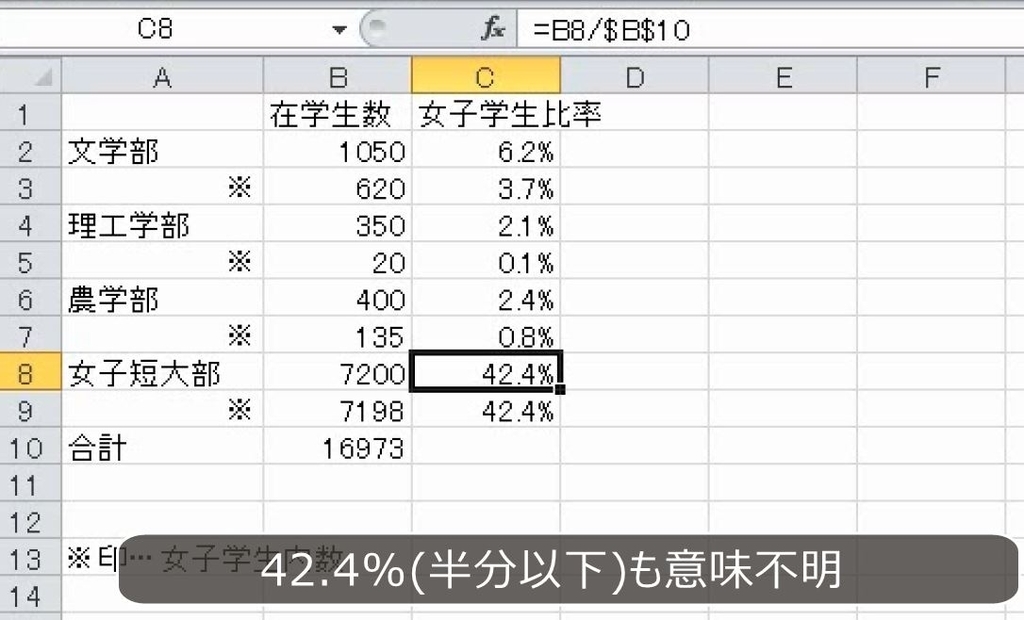
(3)性別なのか学部別なのか
3つ目の回答は全体の合計9000人、女子学生の合計7973人を出して、構成比を求めています。内訳を合計で割っているので正しいように見えます。
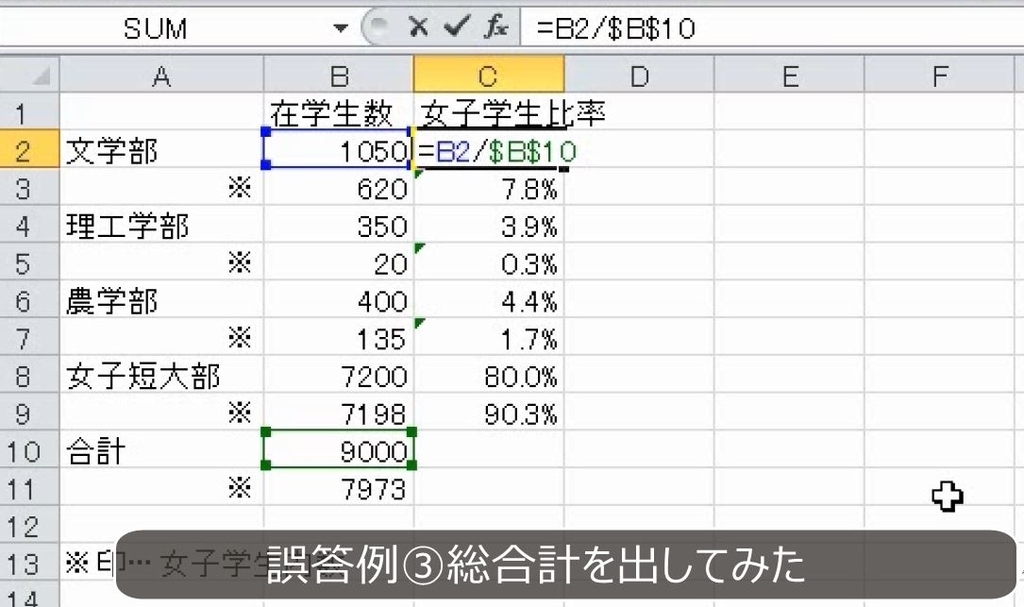
しかし、円グラフをイメージすれば明らかですが、これは、学部の構成比です。短大の学生が多いことを示しているだけで、性別は無関係です。
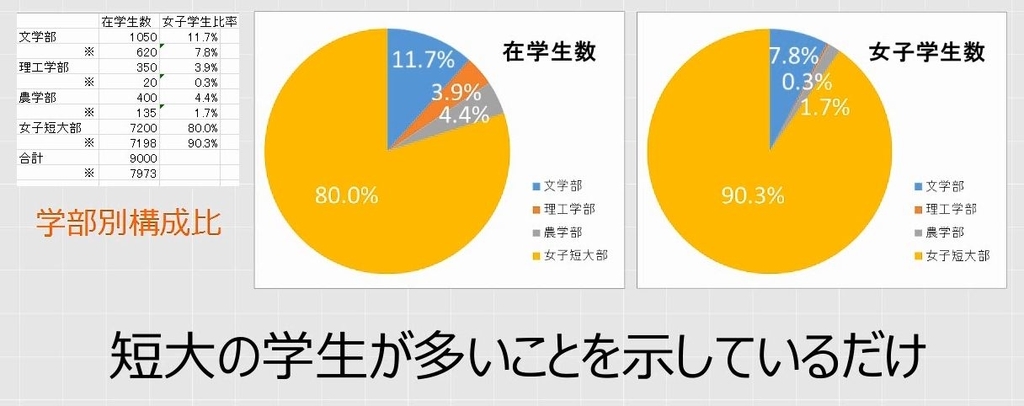
(4)構成比率で何を主張したいのか
また、女子学生だけ求めた4つ目の回答も間違いです。確かに、問題文には「女子学生の構成比」を求めることしか書いていないので、女子学生の内数だけを見て構成比を求めることは、問題文の指示に従っているようにも見えます。

もともと女子学生の構成比を出すのは、男女共学の学校で性別の比率が偏っていないことを示すためであり、女子学生もたくさん通っている(つまり、女子学生向けの施設や設備も整っている)ことをデータで示す意味があります。

誤答例は、女子学生がどの学部に多く属しているかを示しているにすぎず、男女比を表しているわけではありません。このように、構成比を求めるときにはその先の結論を考えて計算する必要があります。
(5)100%の意味
最後に、5つ目の回答は学部ごとに女子学生比率を求めています。これは正しい計算です。
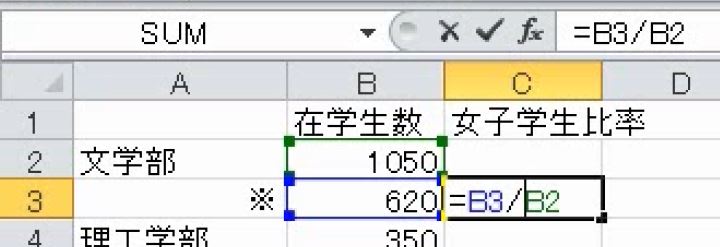
文学部は1050人中620人、約6割が女子学生です。これに対して、理工学部はわずか20人で6%しかいません。男子学生の比率を求めなくても偏っていることが分かります。
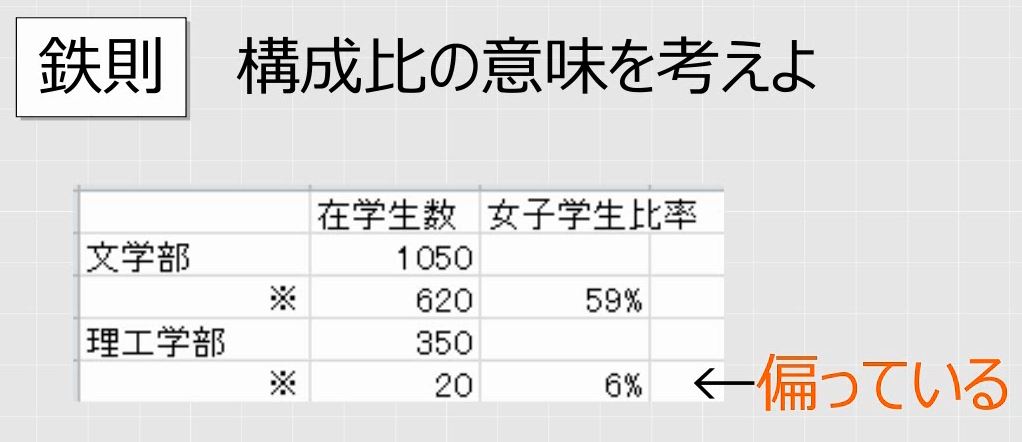
しかし、この表には2か所修正すべき箇所があります。

1つ目は、100%のところです。四捨五入の影響で100%になっていますが、実際には完全に100%ではないので、小数点以下を出すか、注意書きをする必要があります。もう1つは198%です。構成比率は100%を超えることはありません。9000人のうち約8000人ですから90%を切ることは明らかです。

これは縦向きにパーセントを足しているようです。パーセントを足すことができるのは分母が等しい場合に限られます。これらのパーセンテージは分母が違いますので絶対に足してはいけません。

(6)模範解答例
ちなみにこちらが模範解答例です。

5.構成比率の練習問題
(1)稼働率
問題
2500時間運転させた機械が10時間だけ故障のため停止した。稼働率を求めなさい。
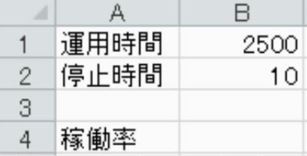
解説
稼働率は、稼働状態とそうではない状態を考えます。構成比率を求めます。

稼働していない時間は2500-10=2490時間です。
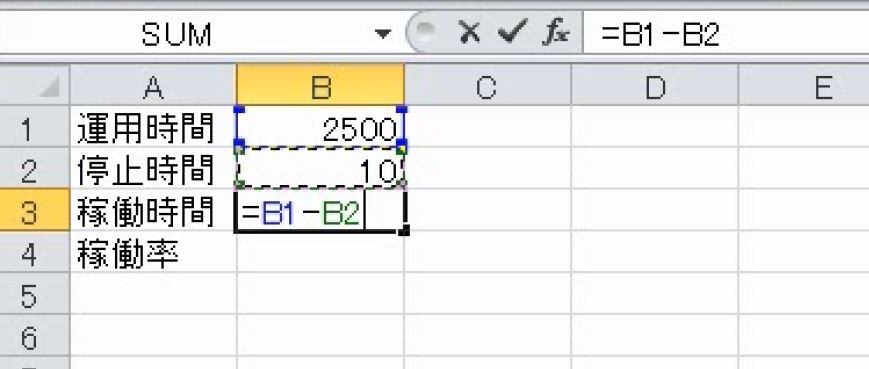
2490時間稼働して、10時間停止していたのですから、2490/2500で99.6%です。

当然稼働している率は100%(=1)に近いほうがいいです。
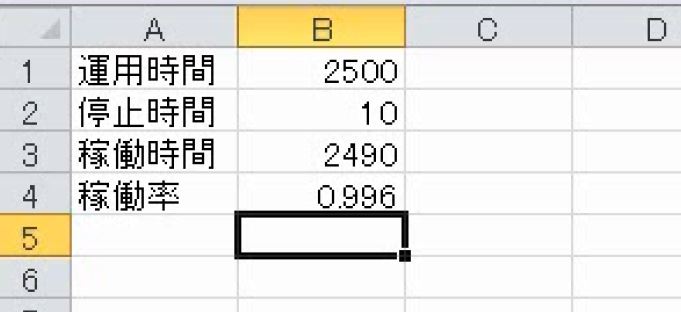
この稼働率のように、構成比率を別の言葉で表現することがあります。YESとNOの2択と考えて、YESとNOで「多い・少ない」を考えながら、該当するほう(YES)の構成比率を出します。

(2)欠席率と合格率
問題
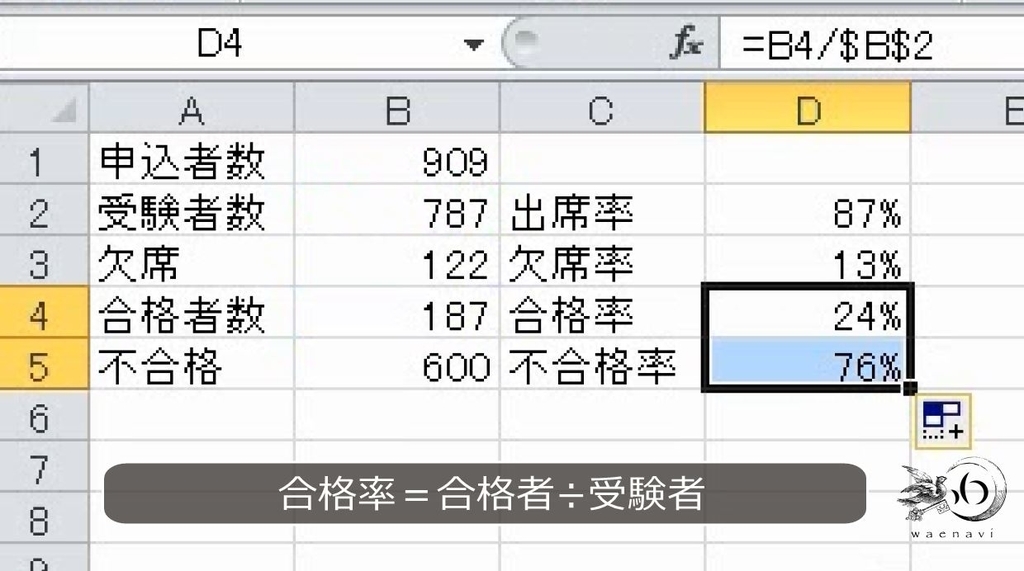
申込者数 909人、受験者数 787人、合格者数 187人のとき、欠席率と合格率を求めなさい。
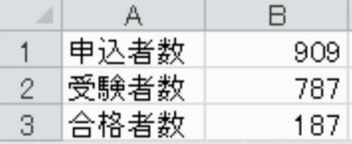
解説
欠席者は、申し込みをしたのに受験しなかった人です。
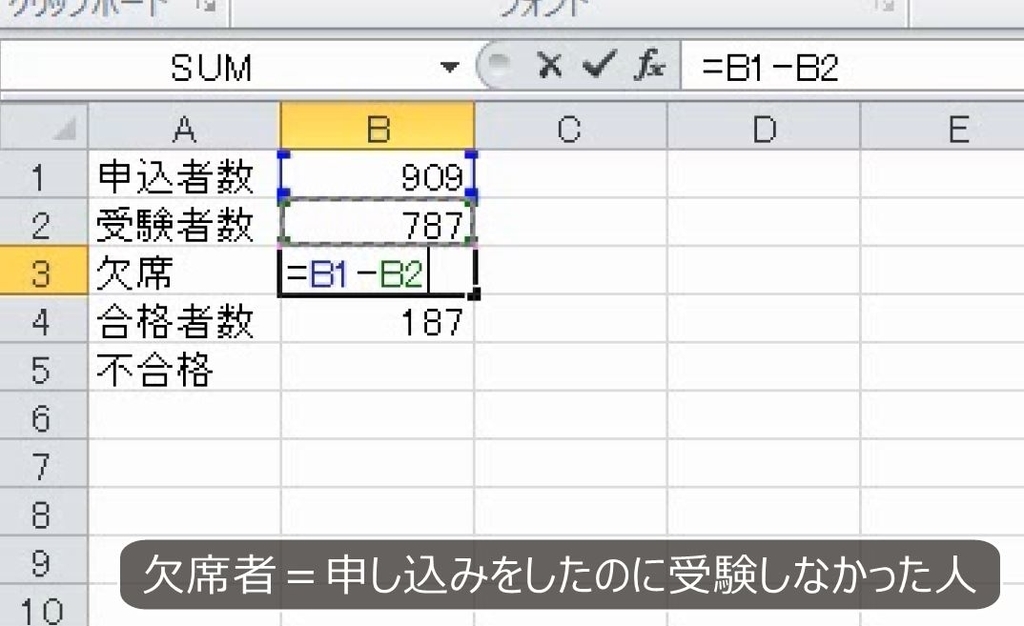
欠席率は欠席した人と、欠席しなかった人(出席して試験を受けた人)を考えます。欠席は122人、出席は787人で合わせて909人です。
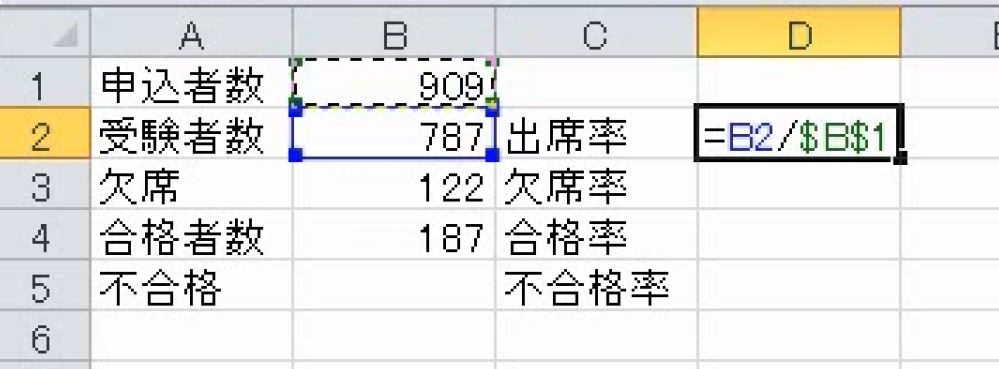
出席率は87%、欠席率は13%です。
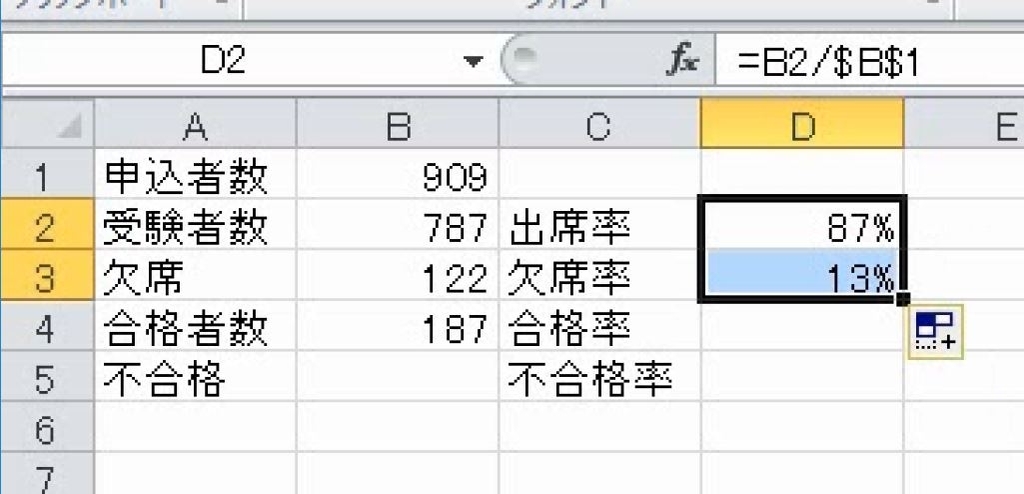
同様に合格者と不合格者で比率を出します。ちなみに、欠席者は棄権扱いで、合格率の計算に入れません。
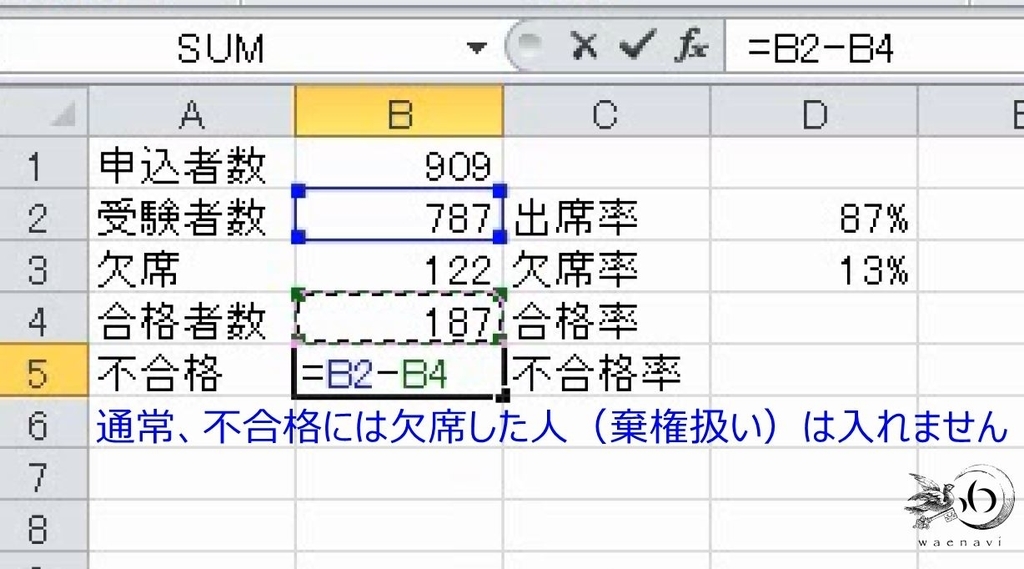
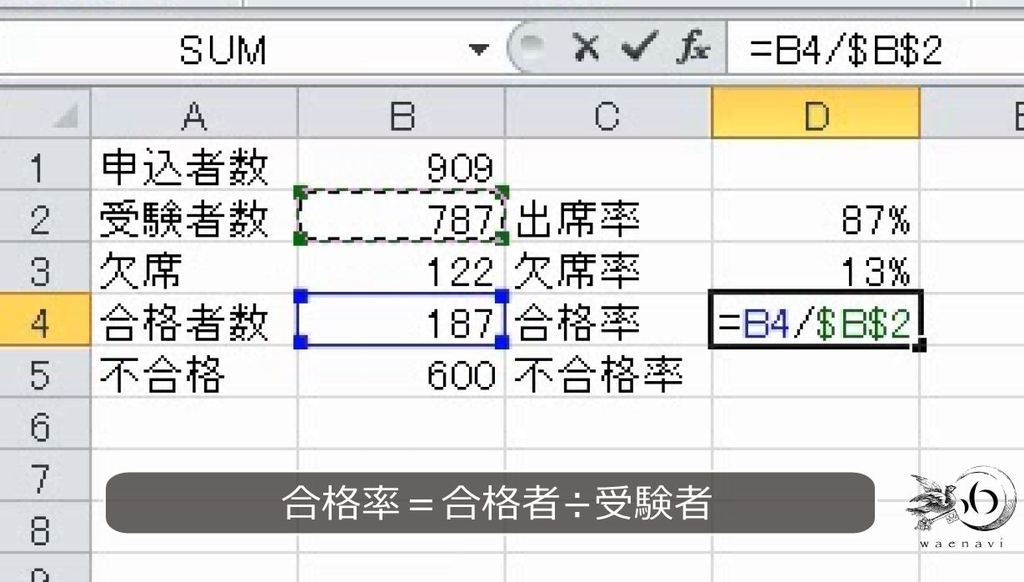
合格率が24%、不合格率が76%です。
(3)カレーライス率
問題
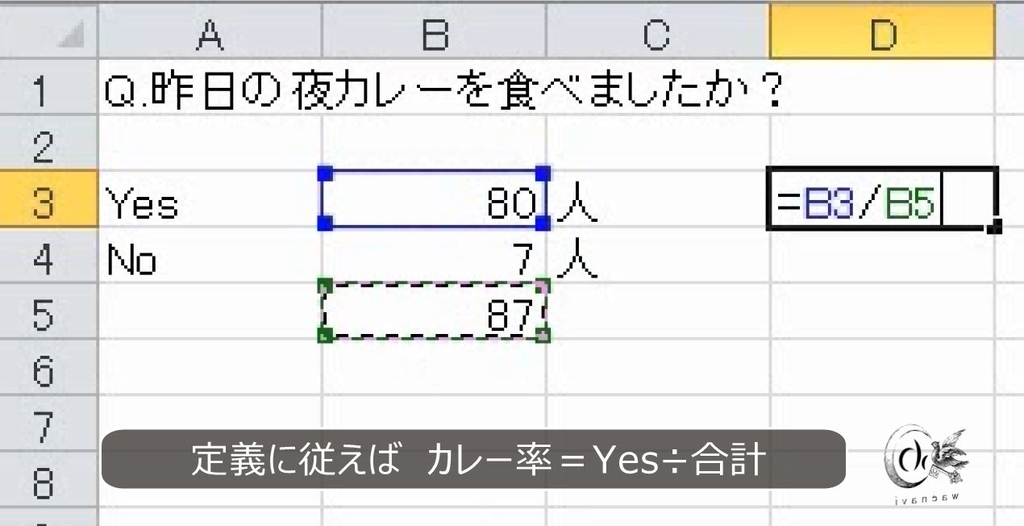
「昨晩カレー率」を「昨日の夜にカレーライスを食べた人の比率」と定義した場合、次の表で昨晩カレー率を求めなさい。

解説
カレーを食べた人と食べてない人、またはカレーが好きな人と嫌いな人に分けて、「カレー率」と名付けたとすれば、その比率を出すことは可能です。このように、YesとNoの2択を用意して、用語を定義すればあらゆる比率を求めることができます。

昨日の夜にカレーライスを食べた人が多いので100%に近い答えになるはずです。構成比率は必ず合計を把握します。
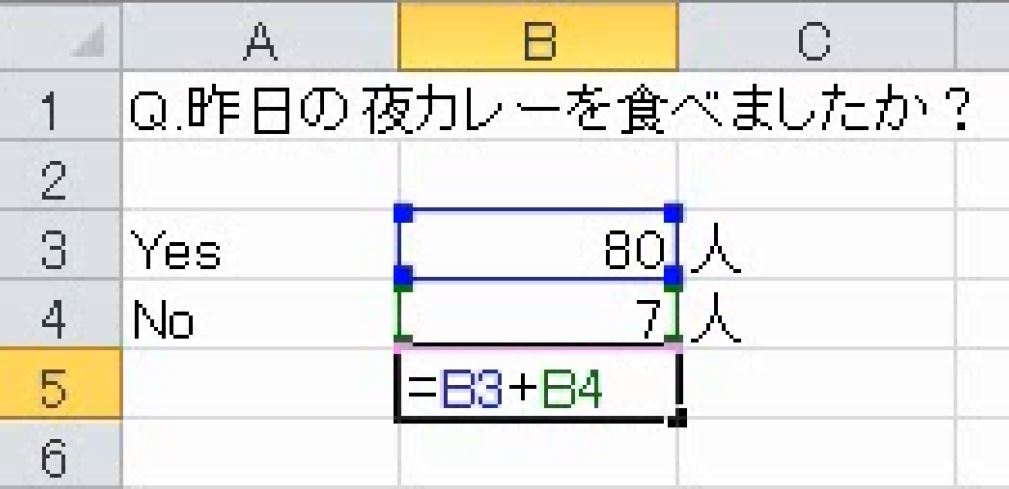
合計87人のうち80人がカレーを食べたので昨晩カレー率は約92%です。
(4)確率
問題
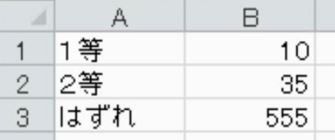
次の表で当たりくじを引く確率を求めなさい。
解説
確率も、考え方は構成比率と同じです。当たりくじを引く確率は、当たるか当たらないかだけを考えて、1等か2等かは気にしてはいけません。
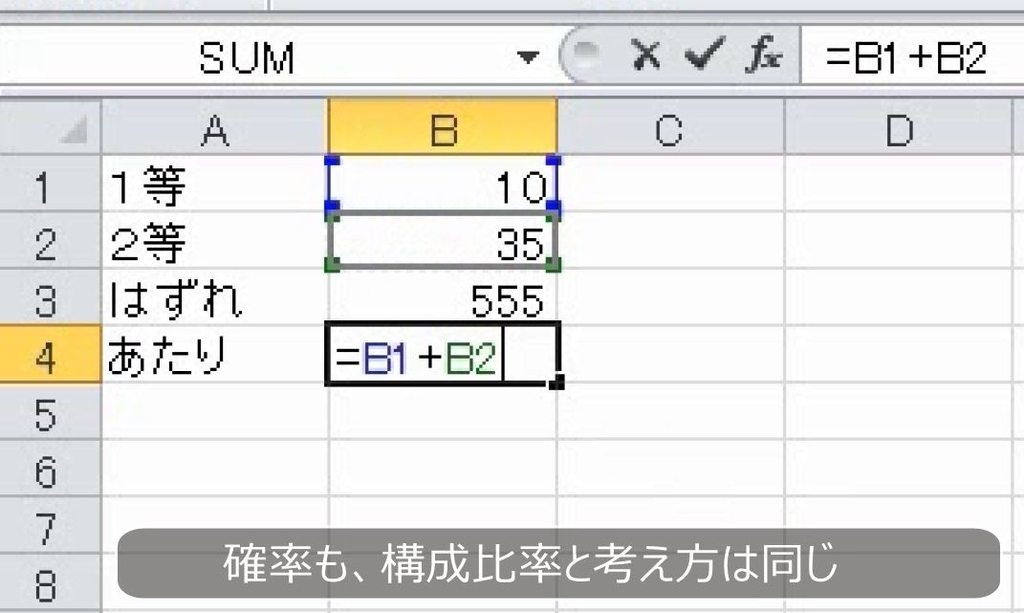
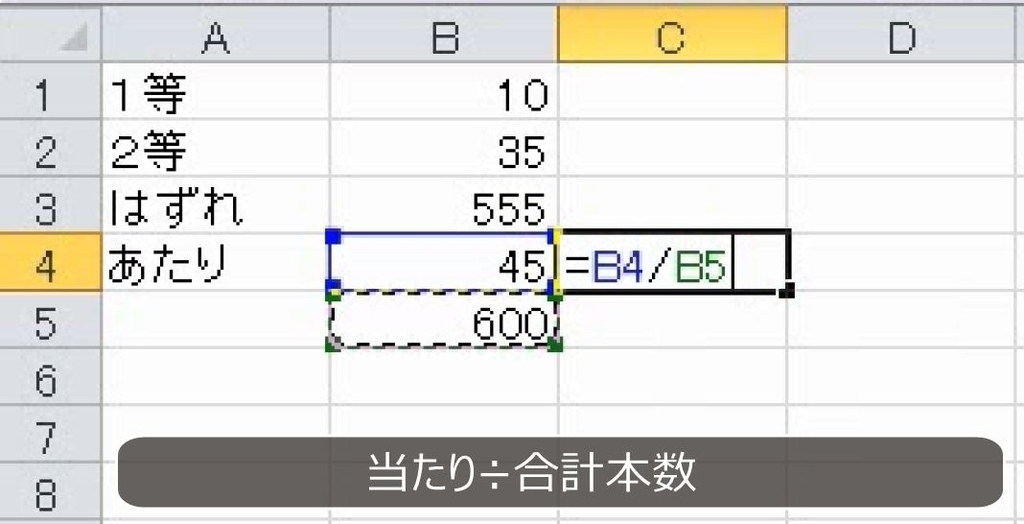
あたりはあわせて45本、あたりとはずれを合わせると全部で600本です。

45/600=7.5%です。
6.合計が増えたら構成比率は下がる
問題
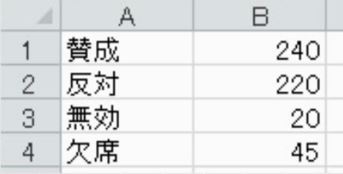
賛成が過半数だったら可決される議案があり、次のような投票結果であった。賛成の比率を求めなさい。
解説
賛成票は240票です。賛成と反対を比較すれば、賛成が多いので可決と考えられます。しかし、無効や欠席者の扱いによって変わってきます。賛成と反対を足します。これは有効投票数です。
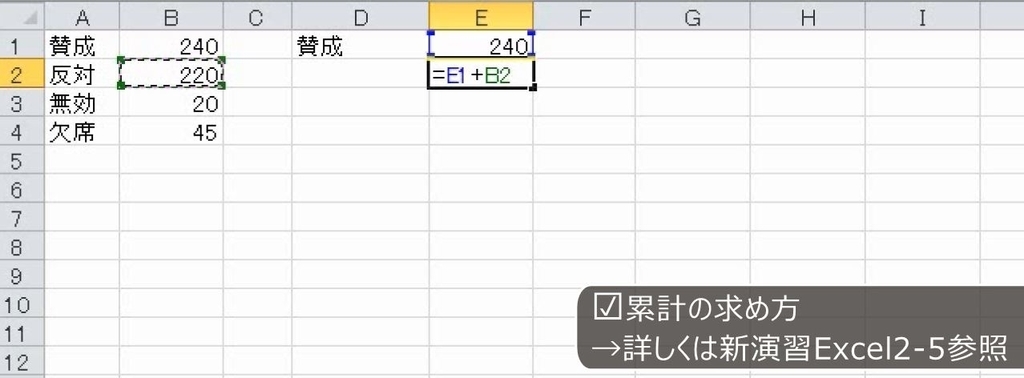
無効票を足すと出席者数です。これに欠席者を足すと総議員数が出ます。
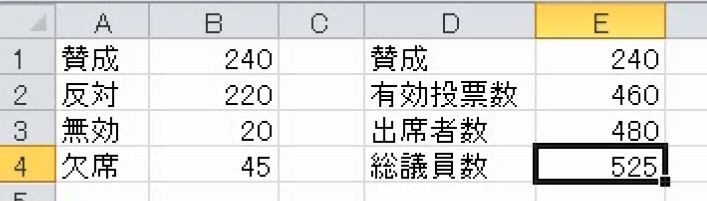
賛成票を絶対参照にして、賛成の比率を求めます。
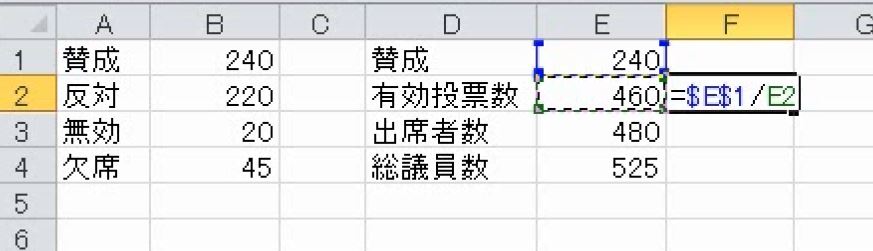
有効投票数を基準にして考えれば、過半数なので可決です。出席者数や総議員数を基準にして考えれば、過半数でないので否決です。合計が大きくなると構成比率は下がります。

7.内訳と構成比率から合計を求める
問題
次の表で、A型の構成比率が40.0%だったと仮定すると、B、O、AB型の構成比率はそれぞれ何%か、Excelを用いて計算しなさい。

解説
構成比率とは全体と内訳を比較したときの比率です。全体を100%としたときに、内訳が何%に当たるかを表した比率で、内訳を全体で割って求めます。

いっぱんに割合をかけるとその割合に相当する量が求められますから、全体に構成比率をかけると内訳になります。比率が40%であれば、それをかけることで40%分の量が求められます。逆に40%で割れば、内訳から全体が求められます。

構成比率が先に分かっている場合、全体から内訳は掛け算で、内訳から全体は割り算で求めます。

438人を40%で割って合計を求めます。
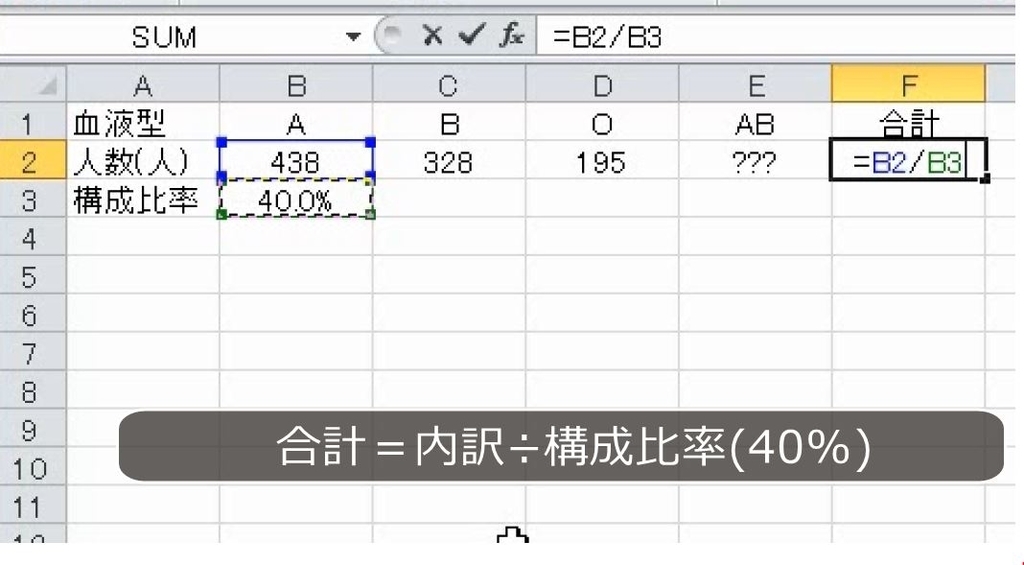
1095人です。AB型の人は、1095人からA、B、Oを引きます。
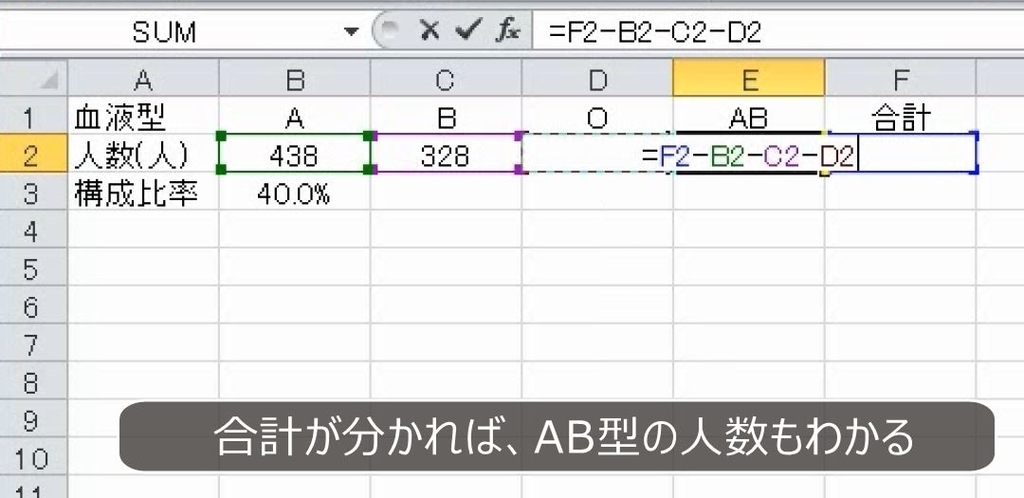
134人となります。これを用いて構成比率を求めます。内訳/合計です。合計は絶対参照です。
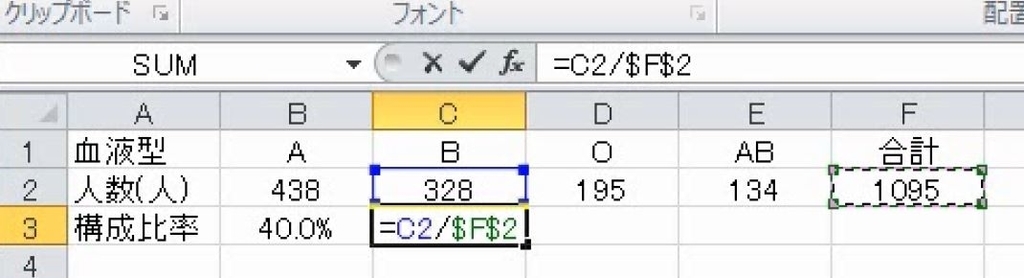
これで完成です。
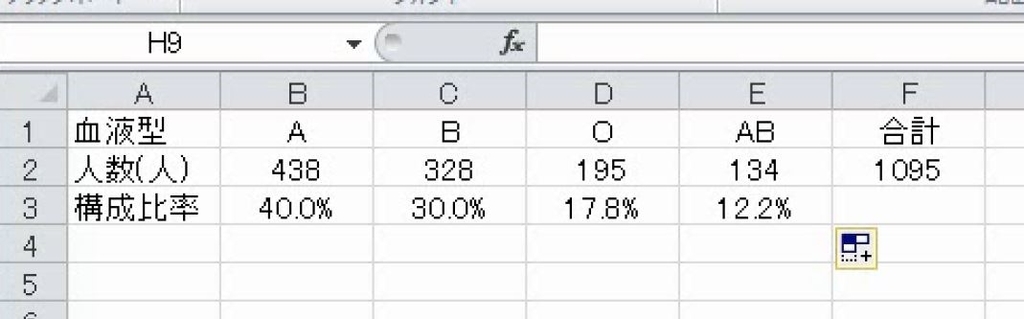
解説は以上です。なお、合計はSUM関数を用いてもかまいません。
8.動画版はこちら(無料)
この記事は、わえなびExcel新演習1割合の重要事例 Program1-6、1-7、1-8、1-6-3 の動画の内容を書き起こし、加筆修正したものです。
- Excel新演習1数式・割合の重要事例 1-6 構成比率1(内訳)
- Excel新演習1数式・割合の重要事例 1-7 構成比率2(構成比の目的)
- Excel新演習1数式・割合の重要事例 1-8 構成比率3(構成比事例演習)
- Excel新演習1数式・割合の重要事例 1-6-3 補講 内訳と構成比率から合計を求める
動画版(完全版)は、Youtubeにすべて無料で公開しております。ぜひ、ご覧ください。
Excel新演習1数式・割合の重要事例(全13回)【わえなび】 - YouTube
https://youtu.be/7PV25yQH5pk?list=PLRaY8kd5CoxN7kDWMfv64FEP_ox3oytHl





