Excelで割合を求めるのが苦手な人は、Excelで数式や関数を打つだけでなく、「なぜそうなるのか?」「その割合が何を表す数値なのか?」を自分の言葉で説明できるようにする習慣をつけたほうが良いです。
そこで、今回は本質的に割合の意味を理解できているかを問うExcelの問題を出題します。ここに載せている問題は、答えよりも理由を自分の言葉で説明できることのほうが大事です。パーセンテージの持つ意味を説明できるようにしましょう。

目次
1.数が増える
問題
次の図は、数値が増えていく様子を表している。この図を見て、Excelを用いて求められる割合をできるだけ多く考えなさい。また、そのようになる理由を述べなさい。

解説
この図の場合、2ずつ増えています。例えば、3人組のアーティストが5人組になると2人増員の影響は大きいですが、東京ドームの観客が2人増えても目立ちません。同じ数だけ増えたとしても、もともとの数(分母)が大きければ、その影響は小さくはずです。
このことを「増加率」として表します。

増加率は、変化後を変化前で割ります。5/3です。
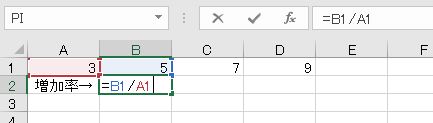
増えた場合は、大きい数を小さい数で割るので、100%を超えます。分母が大きいほうが増加率が低いです。
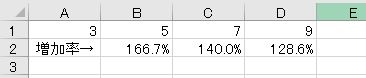
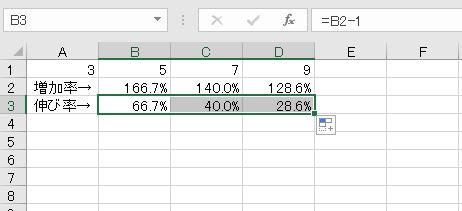
増加分だけを計算する場合は100%にあたる1を引きます。これが「伸び率」です。増えた量は同じですが、伸び率は減ります。もともとの数(分母)が大きければ、伸び率は小さくなります。
2.数が増えたり減ったり
問題
次の図は、最初の数値が7で、いろいろと数値が変わり、最終的に3になる様子を表している。さきほどの問題と同じように、Excelを用いて求められる割合をできるだけ多く考えなさい。また、そのようになる理由を述べなさい。
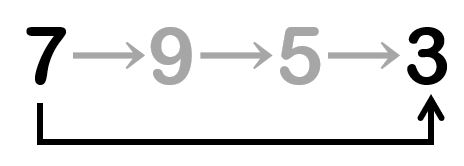
解説
今度は増えたり減ったりしていますが、考え方は同じです。福岡ドームの観客が10人減るよりも、6人組のメンバーが1人減るほうが目立ちます。減った数が多くても、もともとの数がものすごく多ければ影響は少ないはずです。これを「変化率(増加率・減少率)」で表します。変化後を変化前で割ります。100%以上であれば増加、100%未満であれば減少です。
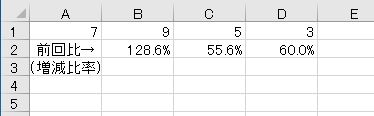
1を引きます。「増減率(伸び率)」です。プラスであれば増加、マイナスであれば減少です。
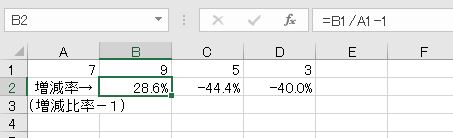
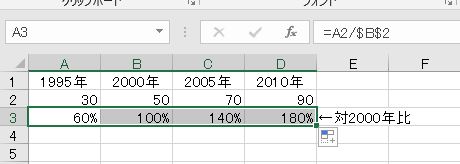
例えば、先月比、前年比、昨年度比のように、過去と比べてどのように変化したかを表す割合は、現在(変化後)を、過去(変化前)で割ります。

また、途中に変動があっても、最初と最後だけを比較して変化率を求めることがあります。この場合も、最後を最初で割ります。途中増えているところがありますが、最終的には減少しているということです。
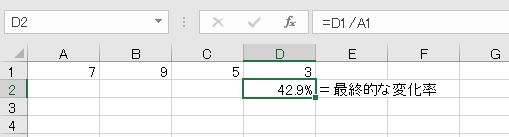
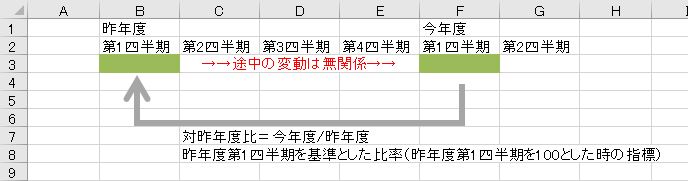
昨年の同じ時期と比較する場合や、ある一時点を基準とした指標を求める場合、途中の変動は関係なく、比較して変化率を求めます。
3.1つを基準として比較する
問題
次の図は、50という数字を中心として、その周りに大きい数や小さい数があるという状況を表している。さきほどの問題と同じように、Excelを用いて求められる割合をできるだけ多く考えなさい。そのようになる理由を述べなさい。
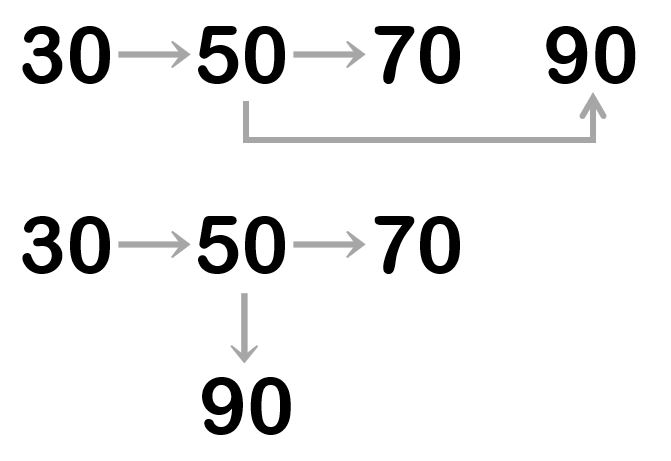
解説
単に数字が並んでいるだけでは、割合を求める意味がありません。例えば、4人の生徒のテストの点を比較するだけであれば、割合という考え方はありません。
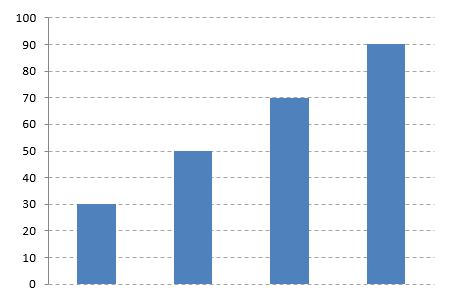
しかし、自分の点数が50点で、他の人がそれより点数が高いか低いかを表すのに割合を用いることはあり得ます。1つだけ基準があれば、それより多い、または、それより少ないということを示す意味があります。これを変化として考えるならば、基準となっているもの(自分の得点)が変化前、それ以外は変化後となります。
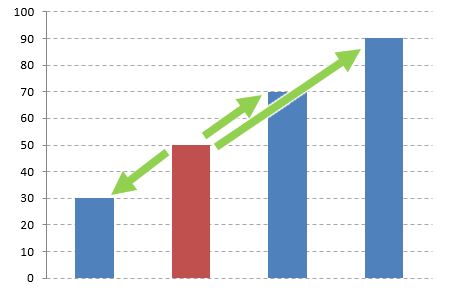
変化後を変化前で割るのは同じです。ただし、基準が1つなので絶対参照になります。
100%未満であればそれより少ない、100%以上であれば基準より多いということです。
基準値は変化がないのは当たり前です。
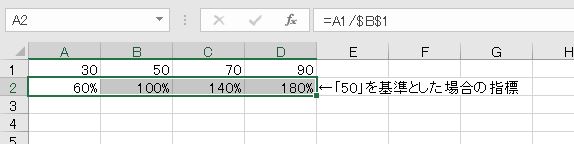
100%にあたる1を引きます。マイナスであればそれより少ない、プラスであれば基準より多いということです。
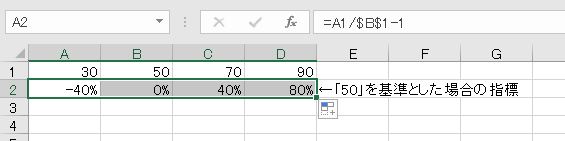
変化する前の量が動けば相対参照、変化する前の基準の量が動かなければ絶対参照です。「対2000年比」は2000年を基準とした比率なので、2000年の数値が基準となる量(絶対参照)となります。
4.内訳
問題
次の図で構成比率を求めなさい。また、「~~率」という言葉で構成比率を表す例をできるだけ多く挙げなさい。

解説
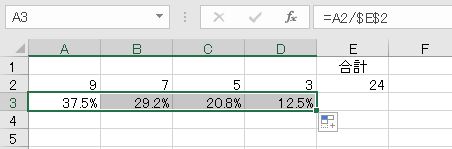
内訳を表す割合の場合、比較するのは内訳と全体の合計です。合計値が基準の量であり、内訳と比較するので、内訳/合計です。合計は24です。これが基準となる量です。
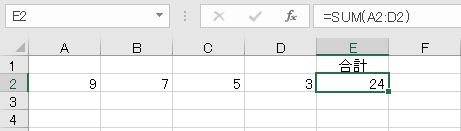
小さい数を大きい数で割ります。
自給率(自給でない=輸入など)、支持率(支持してない=不支持など)、原価率(原価でない=粗利益)のように全体のうちの何%かを表す割合はすべて構成比率です。該当するものとしないもの(YesとNo)にあたるものがあって、その比率を「~~率」という言葉で表せば、それはすべて構成比率です。
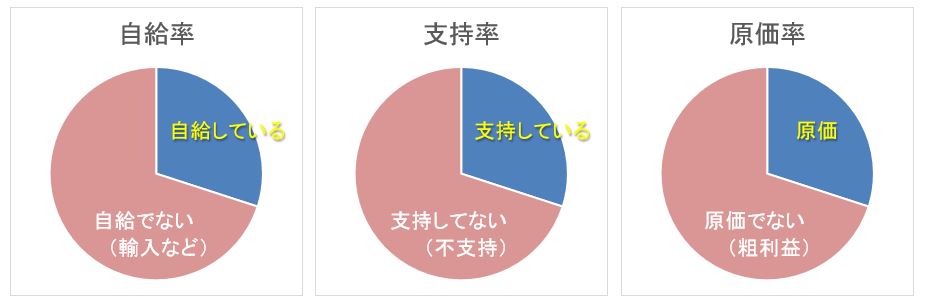
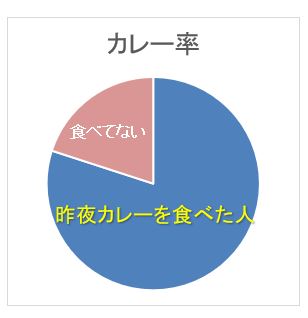
昨夜カレーライスを食べた人の比率を「カレー率」と言うのであれば、カレーを食べていない人との関係で構成比率となります。
5.間違い探し
(1)半分より多い、少ない
問題
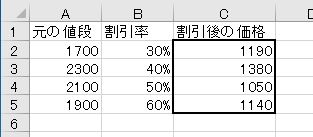
次の図の太枠の部分について、半分より多いか少ないかで考えた場合、1つだけ明らかな誤りがある。理由を付けて指摘しなさい。
解説
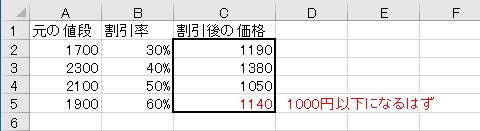
計算結果を見て、その答えが妥当であるかを判断することは非常に重要です。割引率とは、元の値段のうち割引をする金額の部分の割合を表します。
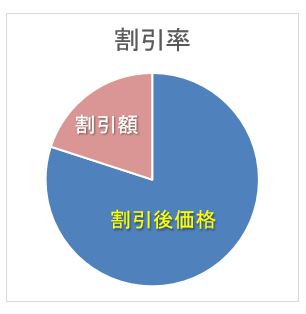
ここで重要なのは「10%」がいくらかということです。10%は、10分の1なので簡単に求められます。1700円の10%引きは170円を引くということです。20%であれば340円引きです。そして、50%引きで半額です。ということは、40%引きであれば半額より多い、60%引きであれば半額より少ないはずです。よって、1900円の半額は950円(少なくとも1000円より少なくなることは明らか)なので、1140円という答えは誤りです。
(2)元の数より多い、少ない
問題
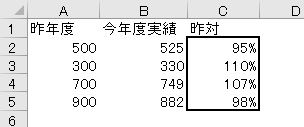
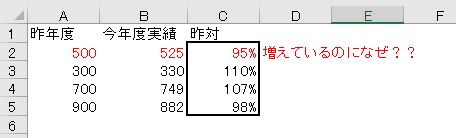
次の図の太枠の部分について、元の数より多いか少ないかで考えた場合、1つだけ明らかな誤りがある。理由を付けて指摘しなさい。
解説
昨対とは「対昨年比」「対昨年度比」「対昨年同月比」などを略した言葉で、昨年を基準として比較しているという意味です。この場合も10%が大事です。昨年度が300で、10%増であれば330、10%減であれば270です。増えていれば100%を超え、減っていれば100%を切っているはずです。500→525は増えているので昨対が95%というのは明らかに誤りです。
6.絶対参照か相対参照か
問題
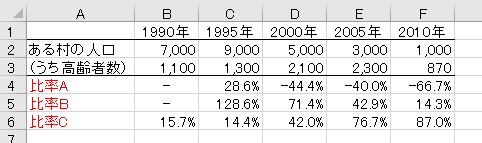
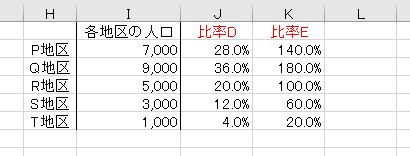
次の2つの表の比率A~Eは、何の比率を求めていると考えられるか、理由を付けて詳しく述べなさい。また、絶対参照を用いる必要があるか述べなさい。
比率A
1つ目の表は、「横向きに時系列の順になっている」というのがポイントです。マイナスのパーセンテージがある場合は「減少」または「小さい」ことを表しています。その後、最初だけプラスでその後にマイナスになっているということは1995年から減少していることを表しています。1995年の28.6%は、村の人口が2000人増加したことを表していると考えられます。そこで10%を考えると、7000人の10%は700人なので、2000人は30%近くとなります。また、-66.7%も半分以上(3分の2)減っていることを表すものであり、計算結果も妥当と考えられます。
よって、比率Aは、5年前と比較した時の増減率を5年ごとに求めているパーセンテージです。「=C2/B2」で相対参照です。
比率B
100%を超えているパーセンテージがある場合、「大きい」または「増えている」ことを表すことが多いです。その後、100%を切っているということは、さきほどの比率Aと同じように1995年から減少していることを表すのが普通です。しかし、最後の14.3%は、3000人と1000人の比較で出てくるパーセンテージではありません。パーセンテージが少なすぎます。ということは、分母が大きいということです(前述)。比率Aの計算結果から、1995年の128.6%は、村の人口が7000人から9000人に増えていることを表しています。7000人の10%は700人なので、「14.3%」はだいたい1000人くらいではないかと考えられます。
よって、比率Bは、1995年と比較した時の比率(対1995年比)です。「=C2/$B$2」で分母は絶対参照です。
比率C
「15.7%」もだいたい1000人くらいなので、高齢者の割合ではないかと考えられます。
その後人口が減る代わりに高齢化が進み、1000人の村人のうち870人が高齢者となっています。これは全体の87%です。
よって、比率Cは、それぞれの年の高齢者の構成比率(高齢者率)です。「=B3/B2」で相対参照です。
比率D
2つ目の表は「項目に時系列が無い」というのがポイントです。通常、時系列ではない項目の数値の隣にパーセンテージがあれば構成比率であることが多いです。すべてのパーセントを足すとだいたい100%になります。Q地区のパーセンテージが多く、T地区が一番少ないことなどから考えても、構成比率を求めていることは明らかです。
よって、比率Dは、5つの地区の人数の合計に対する各地区の構成比率です。「=I2/SUM($I$2:$I$6)」となり、合計は絶対参照です。
比率E
100%を超えているものがあれば「多くなっている」または「増加している」ことを表しますが、時系列が無いので何らかの基準(前述)があってそれと比較していると考えられます。R地区が100%になっていることからR地区が基準となっていることが分かります。
よって、比率Eは、地区Rと比較した時の割合(対R比)を表しています。「=I2/$I$4」で基準となるR地区は絶対参照です。
7.比率を求めてかける
(1)換算比率をかける
問題
「7」→「9」の増加率と同じ割合で5と3をそれぞれ増やしなさい。また、増減率をかける計算の例を挙げなさい。
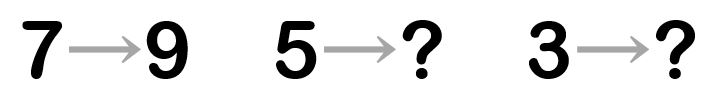
解説
比例計算または換算をするときは必ず、基準となる変化があります。この変化率を求めます。換算後を換算前で割ります。7から9は増えています。増加率は1.28倍です。
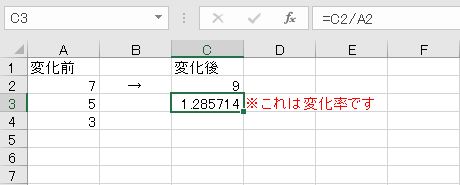
元の数を1.28倍する計算をして増やします。元の数に変化率をかけます。
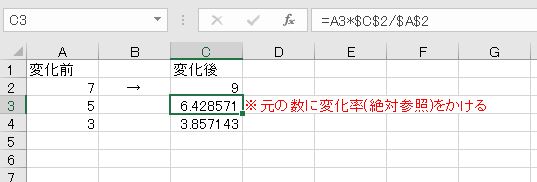
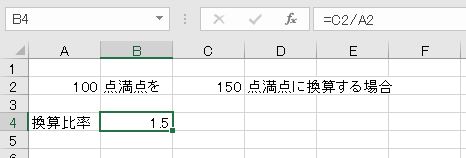
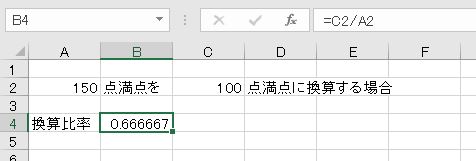
例えば、100点満点を150点満点に換算する場合は、換算によって点数が増えます。増加率は150/100です。逆に150点満点を100点満点に換算する場合は、換算によって減少します。減少率は100/150です。得点や単位を換算するときには、換算比率(増減率)をかけます。
(2)構成比率をかける
問題
「9」を7:5:3に分けなさい。また、比率で分ける計算の例を挙げなさい。
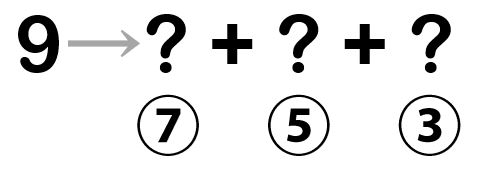
解説
7:5:3のような比率は必ず円グラフを考えます。したがって、求める割合は構成比率です。
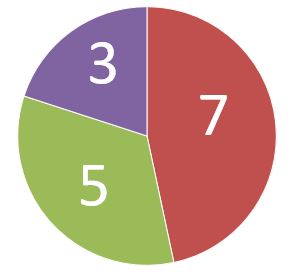
合計を求めます。
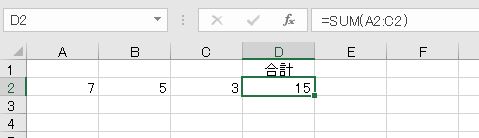
構成比率を求めて、9をかけます。これで完成です。
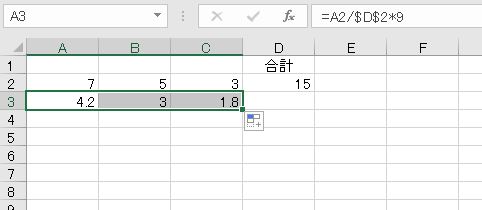
構成比率をかけることによって分けることを按分といいます。按分についてはこちらの記事をご覧ください。
解説は以上です。
7.動画版はこちら(無料)
割合の動画シリーズ(完全版)は、Youtubeにすべて無料で公開しております。ぜひ、ご覧ください。
- Excel新演習1数式・割合の重要事例(全13回)【わえなび】 - YouTube
https://www.youtube.com/playlist?list=PLRaY8kd5CoxN7kDWMfv64FEP_ox3oytHl










