2019秋期基本情報技術者試験の表計算をExcel＆VBAで完全再現してみた！【マクロ】

2019年10月20日(日)に、令和初の情報処理技術者試験（国家試験）が実施されました。
今回から、午前試験で線形代数、確率・統計等、数学に関する出題比率が上がり、理数能力を問う試験に改良されました。とても良い傾向です。

午後試験も、表計算については素直な良問が出題され、Twitterなどでも「簡単だった」「分かりやすかった」という書き込みが多く見られました。最近では小学生でもプログラミングを学ぶ時代なので、今回の問題はExcelでサクッと処理をしてほしいものです。

そこで、Excel＆VBAで再現する方法を紹介しますので、皆さんもメロンをいただきながら作ってみてはいかがでしょうか？

目次

１．出典

試験問題及び正解の著作権はIPA情報処理推進機構に帰属します。

経済産業省国家試験（IPA情報処理推進機構）
令和元年度秋期・基本情報技術者試験・午後試験選択問13表計算
https://www.jitec.ipa.go.jp/1_04hanni_sukiru/mondai_kaitou_2019h31.html#01aki

基本情報技術者午後試験対策書（2020） 情報処理技術者試験対策書 [ アイテックIT人材教育研究部 ]

posted with カエレバ

 

楽天市場

Amazon

Yahooショッピング

 

基本情報技術者らくらく突破表計算　表計算マクロ克服のための擬似言語解説の章を新設！／原山麻美子

posted with カエレバ

 

楽天市場

Amazon

Yahooショッピング

 

２．前半の表計算部分の問題文の要旨

Z組合では、収穫したメロンのうち1kg以上かつ3kg未満のものだけを組合で決めた3等級「優」「良」「並」に分類して直接小売店に出荷している。評価は「優」が最も高く、「並」が最も低い。

1回の出荷ごとに個々のメロンに対してIDを付与する。1回の出荷数は1000個以内とする。等級が「優」「良」のメロンは1個ずつ箱に入れて梱包するが、「並」のメロンは複数個を大箱に入れて梱包する。

３．問題で使用するExcelシートの簡単な作り方

（１）「単価表」シート

これは入力するだけです。

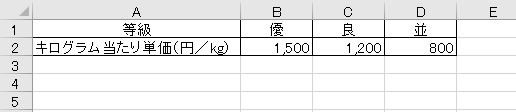
（２）「集計表」シート

形状と表皮色の評価のうち低いほうが、そのメロンの等級となります。算出価格は、「単価表」シートを参照して単価に重量をかけます。また、販売価格は、算出価格を50円単位で切り上げた値です。

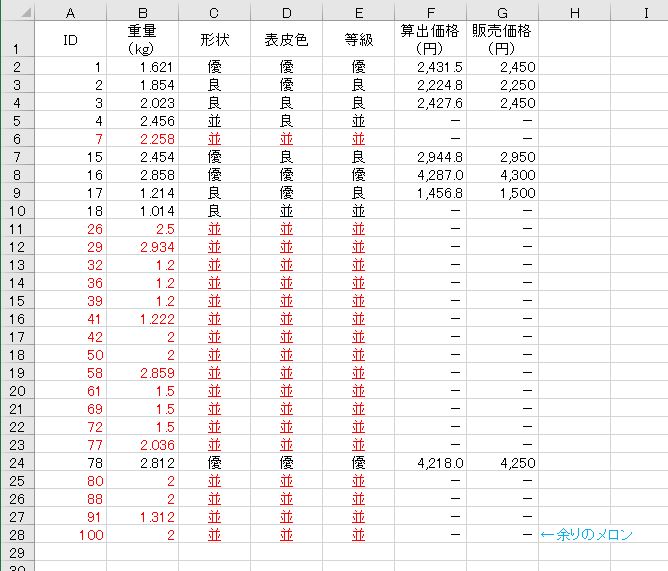
• A～D列：直接入力
• E列：=IF(A2="","",IF(OR(C2="並",D2="並"),"並",IF(OR(C2="良",D2="良"),"良","優")))
• F列：=IF(A2="","",IF(E2="並","－",HLOOKUP(E2,単価表!B$1:D$2,2)*B2))
• G列：=IF(A2="","",IF(E2="並","－",ROUNDUP(F2/50,0)*50))

なお、途中に問題文にない行（赤色のもの）がありますが、これはマクロを再現するためのものです。また、ID=100は箱詰めできない余りのメロンなのでマクロを実行したときには反映されないものです。

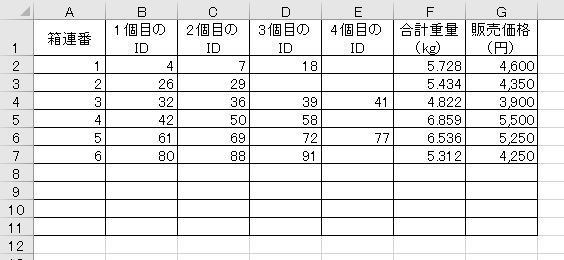
（３）「重量計算表」シート

A2～F1001を空欄にして、マクロ「Packing」を実行します。G列にはメロンの合計重量から販売価格を算出する式を入力しておきます。大箱の販売価格は、メロンの合計重量に「並」の単価をかけて50円単位で切り上げた値です。

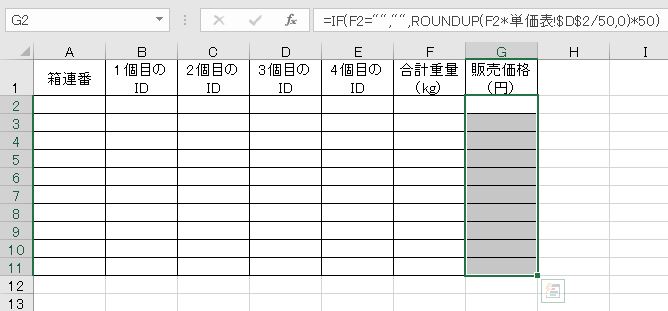
• G列：=IF(F2="","",ROUNDUP(F2*単価表!$D$2/50,0)*50)

４．表計算部分の問題と答え

（１）問題

「集計表」シートのE2、F2、G2に入力する式を答える問題です。Excel２～３級レベルの超基本問題です。

• D4=IF(A2=null,null,[ 解答欄 a ])
• E4=IF(A4=null,null,IF(E2='並','－',[ 解答欄 b ]*B2))
• F4=IF(A4=null,null,IF(E2='並','－',[ 解答欄 c ]))

（２）解答群

aに関する解答群

• ア　IF(論理積(C2='並',D2='並'),'並',IF(論理積(C2='良',D2='良'),'良','優'))
• イ　IF(論理積(C2='優',D2='優'),'優',IF(論理積(C2='並',D2='並'),'並','良'))
• ウ　IF(論理積(C2='優',D2='優'),'優',IF(論理積(C2='良',D2='良'),'良','並'))
• エ　IF(論理和(C2='並',D2='並'),'並',IF(論理和(C2='良',D2='良'),'良','優'))
• オ　IF(論理和(C2='優',D2='優'),'優',IF(論理和(C2='並',D2='並'),'並','良'))
• カ　IF(論理和(C2='優',D2='優'),'優',IF(論理和(C2='良',D2='良'),'良','並'))

bに関する解答群

• ア　照合一致(E2,単価表!$B2:$D2,0)
• イ　照合一致(E2,単価表!B$2:D$2,0)
• ウ　水平照合(E2,単価表!$B2:$D2,2,0)
• エ　水平照合(E2,単価表!B$2:D$2,2,0)
• オ　表引き(単価表!$B2:$D2,2,1)
• カ　表引き(単価表!B$2:D$2,2,1)

cに関する解答群

• ア　切上げ(F2*2,0)/2
• イ　切上げ(F2/2,0)*2
• ウ　切上げ(F2/50,0)*50
• エ　四捨五入(F2,-2)
• オ　四捨五入(F2+50,-2)-50
• カ　四捨五入(F2/50,-2)*50

（３）正解

a－エ、b－エ、c－ウ

（４）解説

いずれの問題も、当サイトの対策問題をやっていれば簡単に答えられる問題でした（参考：基本情報技術者試験の表計算に出題される関数一覧とExcelを用いた簡単な練習方法）。

aについて

形状と表皮色の評価が、それぞれC列とD列に直接入力してあります。これをもとに、低い評価のほうを採用するという設問です。

これは、2通りの方法が考えられます。１つは、論理積(C2='優',D2='優')つまり両方とも優であれば「優」になるという考え方です。「良」になる条件が複雑なので（式が長くなる）、並を考えると論理和(C2='並',D2='並')つまりどちらかが「並」であればよいということになります。したがって、IF(論理積(C2='優',D2='優'),'優',IF(論理和(C2='良',D2='良'),'良','並'))となりますが、これは解答群にありません。

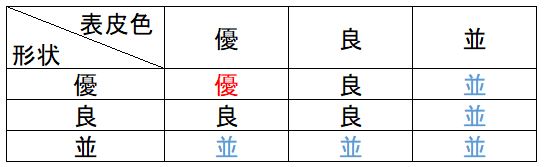
ということは、「優」から考えるのではなく「並」から考えたほうがよいということになります。論理和(C2='並',D2='並')のときに「並」、それ以外の場合、論理和(C2='良',D2='良')のときに「良」とすればよいです。

したがって、「IF(論理和(C2='並',D2='並'),'並',IF(論理和(C2='良',D2='良'),'良','優'))」が正解です。

bについて

優、量、並が1行目にあって、それを検索して単価を求めるのですから水平照合（HLOOKUP）しかないでしょう（参考：垂直照合、水平照合、照合検索、表引き、照合一致の関数を自分の言葉で説明しよう【基本情報技術者試験対策・表計算】）。通常は絶対参照にしますが、数式を下向きにオートフィルをすることを考慮すれば、行固定をすれば十分です。

したがって、「水平照合(E2,単価表!B$2:D$2,2,0)」が正解です。

cについて

50円で切り上げるということは、切り上げた金額は必ず50の倍数になるということです。つまり、求める数式は「整数値＊50」の形になっているはずです（参考：ExcelのINT関数とMOD関数の使い方で最低限理解しておくべき重要事例【基本情報表計算＆Iパス対策】）。この時点で2択（ウとカ）に絞られます。

問題文に切り上げと書いてあるのですから、「切上げ(F2/50,0)*50」が正解です。

５．マクロの概要

1つの大箱には、出荷条件である「メロンの合計重量が5kg以上またはメロンの個数が４個」のどちらかを満たすまでメロンを割り振ります。マクロ「Packing」は次の処理１～４を実行します。

1. A列には、1から順に箱連番を格納する。
2. B～E列には、箱連番が示す大箱に割り振られたメロンのIDを格納する。
3. F列には、合計重量を格納する。
4. 割り振った結果、出荷条件を満たさない大箱に関する情報は、表示しないようにする。

６．マクロ（疑似言語）

[マクロ：Packing]
〇マクロ：Packing
〇数値型：i, j, k, CurrentColumn
・i ← 1
・j ← 1
・CurrentColumn ← 0
■ 相対(集計表!A1, i, 0) <> null
｜▲ 相対(集計表!E1, i, 0) = '並'
｜｜▲ CurrentColumn = 0
｜｜｜・相対(A1, j, 0) ← j
｜｜｜・相対(F1, j, 0) ← 0
｜｜▼
｜｜・相対(B1, j, CurrentColumn) ← 相対(集計表!A1, i, 0)
｜｜・[ 解答欄 d ]
｜｜・CurrentColumn ← CurrentColumn+1
｜｜▲ [ 解答欄 e ]
｜｜｜・j ← j + 1
｜｜｜・CurrentColumn ← 0
｜｜▼
｜▼
｜・i ← i + 1
■
▲ 相対(F1, j, 0) <> null
｜■ k: 0, k<=5, 1
｜｜・[ 解答欄 f ]
｜■
▼

７．マクロの解答群（疑似言語）

dに関する解答群

ア　相対(F1, i, 0) ← 相対(F1, i, 0) + 相対(集計表!B1, 1, 0)
イ　相対(F1, i, 0) ← 相対(F1, i, 0) + 相対(集計表!B1, i, 0)
ウ　相対(F1, i, 0) ← 相対(F1, i, 0) + 相対(集計表!B1, j, 0)
エ　相対(F1, i, 0) ← 相対(F1, j, 0) + 相対(集計表!B1, j, 0)
オ　相対(F1, j, 0) ← 相対(F1, i, 0) + 相対(集計表!B1, 0, 0)
カ　相対(F1, j, 0) ← 相対(F1, j, 0) + 相対(集計表!B1, 0, 0)
キ　相対(F1, j, 0) ← 相対(F1, j, 0) + 相対(集計表!B1, i, 0)
ク　相対(F1, j, 0) ← 相対(F1, j, 0) + 相対(集計表!B1, j, 0)

eに関する解答群

ア　論理積(相対(F1, j, 0) = 5, CurrentColumn = 4)
イ　論理積(相対(F1, j, 0) = 5, CurrentColumn >= 4)
ウ　論理積(相対(F1, j, 0) < 5, CurrentColumn = 4)
エ　論理積(相対(F1, j, 0) >= 5, CurrentColumn < 4)
オ　論理和(相対(F1, j, 0) = 5, CurrentColumn >= 4)
カ　論理和(相対(F1, j, 0) < 5, CurrentColumn = 4)
キ　論理和(相対(F1, j, 0) >= 5, CurrentColumn = 4)
ク　論理和(相対(F1, j, 0) >= 5, CurrentColumn < 4)

fに関する解答群

ア　相対(A1, j, 1) ← null
イ　相対(A1, j, k) ← null
ウ　相対(A1, j, k) ← 相対(A1, j, k) + 1
エ　相対(A1, k, 1) ← null
オ　相対(A1, k, j) ← null
カ　相対(A1, k, j) ← 相対(A1, k, j) + 1

８．マクロの解答

（１）正解

d－キ、e－キ、f－イ

（２）解説

マクロについて

• 集計表のA列をセルA2から下向きにnullになるまでループ
• 集計表のE列が並の場合のみ処理をする
• CurrentColumnが０のとき、A列にj（連番）、F列に０を入れる
• B列～E列に集計表A列のIDを入れる
• [ 解答欄 d ]
• CurrentColumn 1を加算
• [ 解答欄 e ]のときにj に 1を加算して、CurrentColumn を 0にする
• 最後に、F列がnullでなければ[ 解答欄 f ]

変数について

• 「相対(集計表!A1, i, 0)」とあるので、変数「i」は集計表のA列を下向きに数える行番号です。
• 「相対(A1, j, 0)」とあるので、変数「j」はこのシートのA列を下向きに数える行番号です。つまり箱の個数です。
• 「相対(B1, j, CurrentColumn)」とあるので、変数「CurrentColumn」はこのシートのB列から右向きに数える列番号です。つまりメロンの個数です。
• 「k: 0, k<=5, 1」とあるので、変数「k」はこのシートのB列から右向きに数える列番号ではないかと予測できます。

dについて

F列は合計重量を求めていますが、合計を求めるアルゴリズムは必須なので暗記しなければなりません。

・合計の変数 ← 0
■
｜合計の変数 ← 合計の変数 + 数量
■

合計の変数とは合計を格納する場所のことであり「相対(F1, j, 0)」です。数量はメロンの重量であり「相対(集計表!B1, i, 0)」です。

上記の通り、変数の意味が分かっていれば容易に答えが分かるはずです。

eについて

CurrentColumn を 0にするのはなぜかというと、箱の出荷条件を満たしたので、次の箱を用意するからです。したがって[ 解答欄 e ]は出荷条件なので、先ほど求めた合計重量の相対(F1, j, 0) が5以上になるか、またはメロンの個数CurrentColumnが4（または４以上）となります。

fについて

問題文に「出荷条件を満たさない大箱に関する情報は、表示しないようにする。」とあります。これは最後に出荷条件に達しない、余ったメロンがあるということです。しかし、余ったメロンは最終行に残っていますので消す必要があります。

ｋ＝０～５ということはｋが列番号（A列～F列）であることは明らかです。ｊが行番号で、ｋが列番号なので、「相対(A1, j, k) ← null」となります。

９．VBA翻訳に関する補足説明

1. 整数のデータ型はLong型にしています。
2. 標準モジュールではなく、重量計算表シートに格納して実行してください（問題文の指示です）。

10．問題文（VBA翻訳）

Sub Packing()

    Dim i As Long, j As Long, k As Long, CurrentColumn As Long
    i = 1
    j = 1
    CurrentColumn = 0
    Do While Sheets("集計表").Range("A1").Offset(i, 0) <> ""
        If Sheets("集計表").Range("E1").Offset(i, 0) = "並" Then
            If CurrentColumn = 0 Then
                Range("A1").Offset(j, 0) = j
                Range("F1").Offset(j, 0) = 0
            End If
            Range("B1").Offset(j, CurrentColumn) = Sheets("集計表").Range("A1").Offset(i, 0)
            [ 解答欄 d ]
            CurrentColumn = CurrentColumn + 1
            If [ 解答欄 e ] Then
                j = j + 1
                CurrentColumn = 0
            End If
        End If
        i = i + 1
    Loop
    If Range("F1").Offset(j, 0) <> "" Then
        For k = 0 To 5
            [ 解答欄 f ]
        Next
    End If

End Sub

11．解答群（VBA翻訳）

dに関する解答群

ア　Range("F1").Offset(i, 0) = Range("F1").Offset(i, 0) + Sheets("集計表").Range("B1").Offset(1, 0)
イ　Range("F1").Offset(i, 0) = Range("F1").Offset(i, 0) + Sheets("集計表").Range("B1").Offset(i, 0)
ウ　Range("F1").Offset(i, 0) = Range("F1").Offset(i, 0) + Sheets("集計表").Range("B1").Offset(j, 0)
エ　Range("F1").Offset(i, 0) = Range("F1").Offset(j, 0) + Sheets("集計表").Range("B1").Offset(j, 0)
オ　Range("F1").Offset(j, 0) = Range("F1").Offset(i, 0) + Sheets("集計表").Range("B1").Offset(0, 0)
カ　Range("F1").Offset(j, 0) = Range("F1").Offset(j, 0) + Sheets("集計表").Range("B1").Offset(0, 0)
キ　Range("F1").Offset(j, 0) = Range("F1").Offset(j, 0) + Sheets("集計表").Range("B1").Offset(i, 0)
ク　Range("F1").Offset(j, 0) = Range("F1").Offset(j, 0) + Sheets("集計表").Range("B1").Offset(j, 0)

eに関する解答群

ア　Range("F1").Offset(j, 0) = 5 And CurrentColumn = 4
イ　Range("F1").Offset(j, 0) = 5 And CurrentColumn >= 4
ウ　Range("F1").Offset(j, 0) < 5 And CurrentColumn = 4
エ　Range("F1").Offset(j, 0) >= 5 And CurrentColumn < 4
オ　Range("F1").Offset(j, 0) = 5 Or CurrentColumn >= 4
カ　Range("F1").Offset(j, 0) < 5 Or CurrentColumn = 4
キ　Range("F1").Offset(j, 0) >= 5 Or CurrentColumn = 4
ク　Range("F1").Offset(j, 0) >= 5 Or CurrentColumn < 4

fに関する解答群

ア　Range("A1").Offset(j, 1) = ""
イ　Range("A1").Offset(j, k) = ""
ウ　Range("A1").Offset(j, k) = Range("A1").Offset(j, k) + 1
エ　Range("A1").Offset(k, 1) = ""
オ　Range("A1").Offset(k, j) = ""
カ　Range("A1").Offset(k, j) = Range("A1").Offset(k, j) + 1

12．正解を入れた完全版（VBA翻訳）

Sub Packing()

    Dim i As Long, j As Long, k As Long, CurrentColumn As Long
    i = 1
    j = 1
    CurrentColumn = 0
    Do While Sheets("集計表").Range("A1").Offset(i, 0) <> ""
        If Sheets("集計表").Range("E1").Offset(i, 0) = "並" Then
            If CurrentColumn = 0 Then
                Range("A1").Offset(j, 0) = j
                Range("F1").Offset(j, 0) = 0
            End If
            Range("B1").Offset(j, CurrentColumn) = Sheets("集計表").Range("A1").Offset(i, 0)
            Range("F1").Offset(j, 0) = Range("F1").Offset(j, 0) + Sheets("集計表").Range("B1").Offset(i, 0)
            CurrentColumn = CurrentColumn + 1
            If Range("F1").Offset(j, 0) >= 5 Or CurrentColumn = 4 Then
                j = j + 1
                CurrentColumn = 0
            End If
        End If
        i = i + 1
    Loop
    If Range("F1").Offset(j, 0) <> "" Then
        For k = 0 To 5
            Range("A1").Offset(j, k) = ""
        Next
    End If

End Sub

13．結論：わえなび的な講評

今回の問題は、メロンの箱詰めという分かりやすい題材で、「メロンが良かった」「メロンが食べたくなった」という意見も見受けられました。こういう親しみやすい問題というのは非常に良いと思いました。

平成28年から30年にかけて、複雑な表と不可解なアルゴリズムの問題が連続して出題されていましたが、前回平成31年春はシンプルな良問でした（参考：2019春期基本情報技術者試験の表計算をExcel＆VBAで完全再現してみた！）。

前回はシート4枚（表が4つ）でしたが、今回はシート3枚（表が3つ）となりさらにシンプルになりました。いわゆる神エクセルのような複雑な表もなく良問と言えます。しかしながら、前回出題された二次元配列は今回は出題されませんでした。1次元配列もなく、二重ループもないというあっさりとした問題でした。解答群についても消去法であっさり答えがでてしまい、「易化」と言えるでしょう。できれば配列は出題してほしかったです。

次回2020年春試験から表計算（ソフト開発）の配点が20点から25点に引き上げられます。100点満点のうち50点がアルゴリズムの問題となります（すばらしい！！）。次回以降もプログラミング能力を重視した出題を期待します。

過去の問題の完全再現（VBAのみ）はこちら。

note.com