直角三角形で最も有名な公式である三平方の定理(ピタゴラスの定理)は中学3年の数学で学習します。三角関数については別の記事ですでに解説していますが、ATAN関数で直角三角形の角度を求めることができます(参考:Excelの三角関数(SIN・COS・TAN)の具体的な使い方と注意点【サインコサインタンジェント】)。
三平方の定理は、「直角三角形の斜辺の長さは、他の2辺の長さの2乗の和である」というものですが、Excelで、2乗やルートの計算ができれば辺の長さを求めることができます。また、直方体やxyz座標のような3次元空間でも三平方の定理を使います。
そこで、今回は、直角三角形の辺の長さと角度に関する問題と、三平方の定理を用いた応用問題を出題します。
目次
1.三平方の定理(ピタゴラスの定理)
問題
Excelで次の図を描き、三平方の定理を説明しなさい。

解説
セルに斜めの罫線を引くことができますから、罫線を用いて直角三角形を描くこともできます(参考:Excelで斜めの罫線を引いて文字を入れる表の練習問題集)。

三平方の定理の証明方法は100個以上あるといわれていますが、最も有名な証明は直角三角形を4つ並べる方法です。
斜辺の長さをc、それ以外の2辺の長さをa、bとすると、大きい正方形の面積は(a+b)2、小さい正方形の面積はc2で、直角三角形の面積はab/2 なので、(a+b)2=c2+ab/2 *4となり、両辺から2abを引くとa2+b2=c2となります。
2.直角三角形の斜辺、2辺の長さ、面積
問題
Excelを用いて直角三角形の辺の長さと面積を求めようとしている。
C列に斜辺の長さを入力し、A列とB列にその他の2辺の長さを入力するとき、残りの辺の長さを求めなさい。また、面積を求めなさい。

解説
直角三角形の3編の長さのうち2つが分かっていれば、残りの1つを求めることができます。2辺の長さが分かっていれば、2乗+2乗のルートです。Excelで2乗は「^2」、ルートは「^0.5」です(参考:【Excel】逆数と反数、平方根、累乗は初心者の段階で習得すべき_数式の基本)。
=(A2^2+B2^2)^0.5 と入力します。

2辺の長さが5と12のとき、斜辺の長さは13となります。

斜辺が分かっているときは、2乗-2乗のルートです。=(C3^2-A3^2)^0.5と入力します。ルートなので小数になることもあります。

同様に、=(C4^2-B4^2)^0.5と入力します。

面積は底辺*高さ/2です。

3.二等辺三角形
(1)二等辺三角形の高さと面積
問題
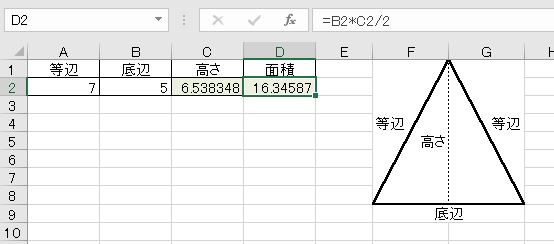
3辺の長さが7、7、5の二等辺三角形の高さと面積を求めなさい。

解説
二等辺三角形の等しい辺(等辺)は直角三角形の斜辺にあたります。底辺は半分にします。斜辺の長さが分かっているので、高さは2乗ー2乗です。

=(A2^2-(B2/2)^2)^0.5 と入力します。

面積は底辺*高さ/2です。
(2)正三角形
問題
A列に正三角形の1辺の長さを入力した。B列に高さ、C列に面積を求めなさい。

解説
二等辺三角形と同じように2乗ー2乗で高さを求めます。=(A2^2-(A2/2)^2)^0.5 と入力します。

面積は底辺*高さ/2です。

別解
正三角形の高さは、1辺の長さの(ルート3)/2倍です(sin60°)。

A列に3^0.5/2をかけます。

面積は1辺の長さの2乗の 3^0.5/4 倍です(sin60°/2)。
- =A2^2*3^0.5/4

(3)円すい
問題
母線=7、底面の半径=4の円錐の高さと体積を求めなさい。

解説
円錐を縦に切断すると断面は二等辺三角形です。円錐の母線が直角三角形の斜辺にあたります。斜辺の長さが分かっているので、高さは2乗ー2乗です。

=(A2^2-B2^2)^0.5 と入力します。

体積は半径^2*円周率*高さ/3です。円周率は「PI()」です。

4.直方体の対角線の長さ
問題
(1)縦=5、横=7、高さ=6の直方体の対角線の長さを求めなさい。
(2)1辺の長さ=15の立方体の対角線の長さを求めなさい。

解説
直方体の対角線とは、直方体の中心を通って、反対側にある頂点同士を結ぶ線のことですが、この長さは2乗+2乗+2乗のルートです。

=(B1^2+B2^2+B3^2)^0.5 です。

縦、横、長さをすべて15にすると、立方体の対角線の長さになります。

別解
立方体の対角線の長さは、1辺の長さのルート3倍です。3^0.5をかけます。

5.2点間の距離
(1)2次元の座標
問題
xy座標平面上に2点A、Bがあり、それぞれのx座標、y座標を入力した。2点間の距離を求めなさい。

解説
x座標同士の差とy座標同士の差が直角三角形の2辺であり、求める2点間の距離は斜辺にあたります。したがって、三平方の定理が使えます。
- ( (x座標の差)^2+(y座標の差)^2)^0.5

=( (A3-C3)^2+(B3-D3)^2 )^0.5と入力します。

(2)3次元の座標
問題
xyz座標空間に2点A、Bがあり、それぞれのx座標、y座標、z座標を入力した。
2点間の距離を求めなさい。

解説
平面の場合は直角三角形として考えられますが、空間の場合は直方体の対角線として考えられます。x座標の差、y座標の差、z座標の差が直方体の縦、横、高さであり、求める2点間の距離は対角線にあたります。したがって、三平方の定理が使えます。
- ( (x座標の差)^2+(y座標の差)^2+(z座標の差)^2 )^0.5
=( (A3-D3)^2+(B3-E3)^2+(C3-F3)^2 )^0.5と入力します。

6.直角三角形の底辺と高さと角度の計算(TAN関数)
問題
直角三角形の高さ、底辺、鋭角の角度のうち2つが分かっていれば残り1つを求めることができる。空欄を求めなさい。

解説
底辺(横幅)の長さに対する、高さの比率をtan(タンジェント)といいます。
- tan = 高さ/底辺

底辺が分かっていれば、tanを掛けることで高さを求めることができます。ExcelでtanはTAN関数ですが、引数はラジアン(弧度法)なのでRADIANS関数で囲む必要があります(参考:Excelの三角関数(SIN・COS・TAN)の具体的な使い方と注意点)。
- 高さb = 底辺a*TAN
- =B2*TAN(RADIANS(C2))

逆に、高さから底辺を求めるにはTANで割ります。
- 底辺a = 高さb/TAN
- =A3/TAN(RADIANS(C3))

高さが5、底辺が7のとき、TAN=5/7です。TANが分かっているときの角度を、arctan(アークタンジェント)といいます(参考:【Excel】三角関数と逆三角関数で、三角形の辺の長さや角度を求める方法まとめ)。
- 角度 = arctan(TAN)

ExcelではATAN関数です。ただし、答えはラジアンなので度数法になおします。度数に直す関数はDEGREES関数です。
- =DEGREES(ATAN(A4/B4))
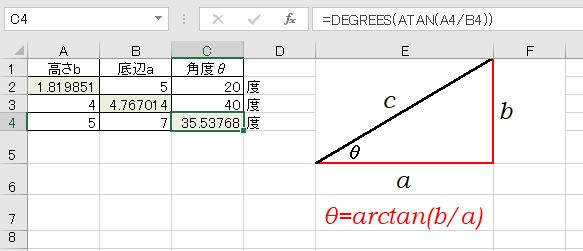
ちなみに、直角三角形の直角以外の2つの角の和は90°なので、90から角度を引けば残りの角度を求めることができます。

解説は以上です。
