三角関数にはsin、cos、tanのほか、逆三角関数(arcsin、arccos、arctan)、割三角関数(sec、cosec、cot)、双曲線関数(sinh、cosh、tanh)などたくさんあってこのブログでは紹介しきれないくらいあります。基本的には、角度から辺の長さを求めるには三角関数を使い、辺の長さから角度を求めるには逆三角関数を使えばよいです。
逆三角関数を使うには、少なくとも三平方の定理と三角比の基本は知っておかなければなりません。
今回は、Excelに搭載されている三角関数のうち、三角関数の基本と逆三角関数と割三角関数について解説します。
目次
1.円周率と弧度法
(1)PI関数
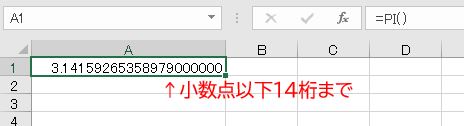
PI関数(パイ)は円周率πを返します。ただし、Excelの有効数字は15桁なので、表示されるのは最大で小数点以下14桁までです。固定の値を返すので、引数はありません。
- =PI()
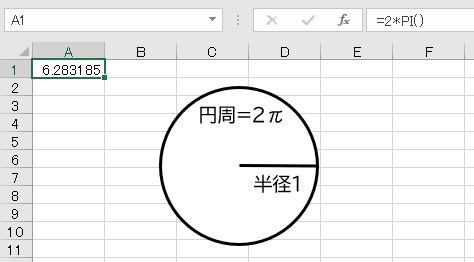
円周の長さは、直径*円周率です。例えば、半径1の円の円周の長さは2πです。この円周の長さは後述のラジアンと関係しています。
- =2*PI()
(2)RADIANS関数
1回転を360度とする角度のことを度数法というのに対して、1回転を2πとする角度のことを弧度法(ラジアン)といいます。「360度=2πラジアン」です。角度をラジアンにするには、π/180を掛けます。

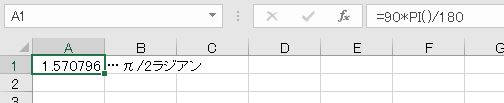
90度をラジアンにすると、90*π/180=π/2ラジアンとなります。
- =90*PI()/180
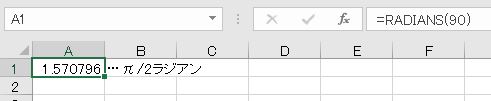
RADIANS関数は角度をラジアンに換算します。つまり、π/180を掛けるだけの関数です。
- =RADIANS(90)
(3)DEGREES関数
「360度=2πラジアン」なので、ラジアンを角度にするには、180/πを掛けます。
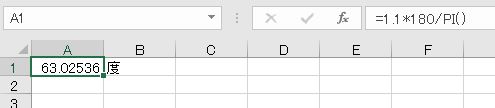
1.1ラジアンを角度にすると、1.1*180/π=約63度となります。
- =1.1*180/PI()
DEGREES関数(ディグリーズ)はラジアンを角度に換算します。つまり、180/πを掛けるだけの関数です。
- =DEGREES(1.1)

2.三角関数
(1)三角関数の引数はラジアン
三角比は、直角三角形の辺の比率を表した値です(参考:Excelの三角関数(SIN・COS・TAN)の具体的な使い方と注意点【サインコサインタンジェント】)。
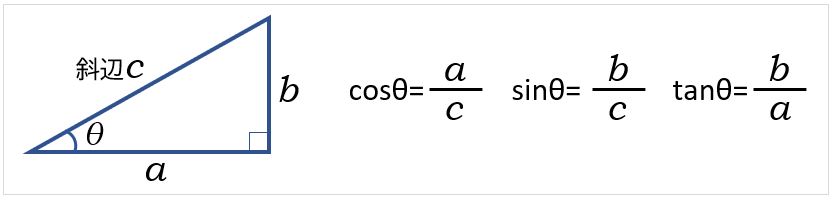
そして、斜辺の長さを1とすると、底辺の長さがcosθ、高さがsinθとなり、その傾きを示す値がtanθとなります。
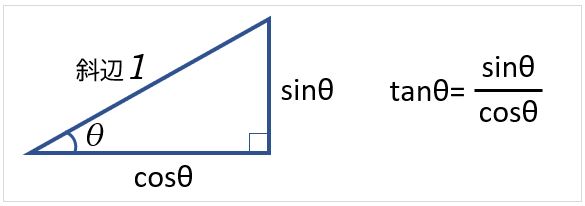
さらに、90度以上の角度に拡張して、原点Oを中心とする半径1の円周(単位円)上の点を(cosθ,sinθ)としたのが三角関数です。x座標がcosθ、y座標がsinθ、線を伸ばしてx座標が1のときのy座標がtanθです。
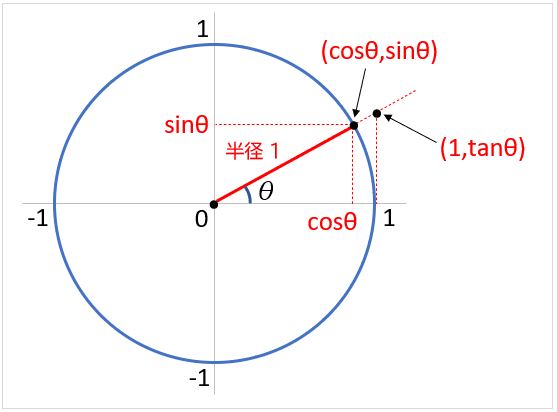
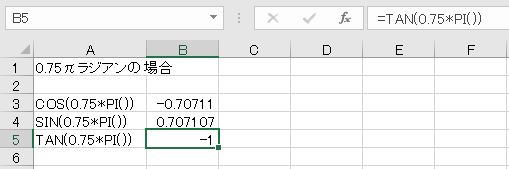
0.75πラジアン(=135度)の場合、cos、sin、tanは、COS関数、SIN関数、TAN関数を用いて、それぞれ次のように求めることができます。
- =COS(0.75*PI())
- =SIN(0.75*PI())
- =TAN(0.75*PI())
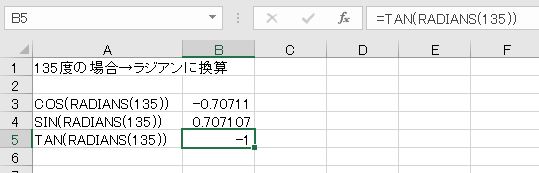
これらの関数は引数をラジアンにしなければならないことに注意します。度単位の場合は、180/πを掛けるか、RADIANS関数を用いてラジアンに換算しなければなりません。
- =COS(RADIANS(135))
- =SIN(RADIANS(135))
- =TAN(RADIANS(135))
(2)直角三角形の場合
問題
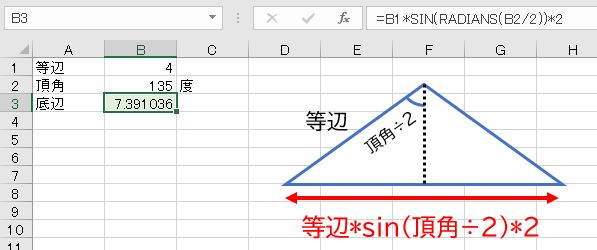
等辺=4、頂角=135度の二等辺三角形の底辺の長さを求めなさい。

解説
二等辺三角形を半分にすると直角三角形になります。直角三角形の場合は、三角比の定義がそのまま使えます。等辺にsinをかけると向かい合う辺(底辺の半分)の長さを求めることができます。
- 底辺の半分=等辺*sin(頂角の半分)
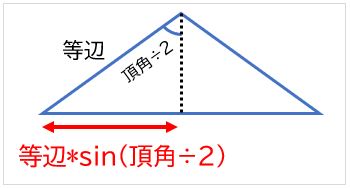
それを2倍すれば底辺の長さになります。ラジアンにするのを忘れてはいけません。
- =B1*SIN(RADIANS(B2/2))*2
- =B1*SIN(B2*PI()/180)*2
(3)直角三角形でない場合
問題
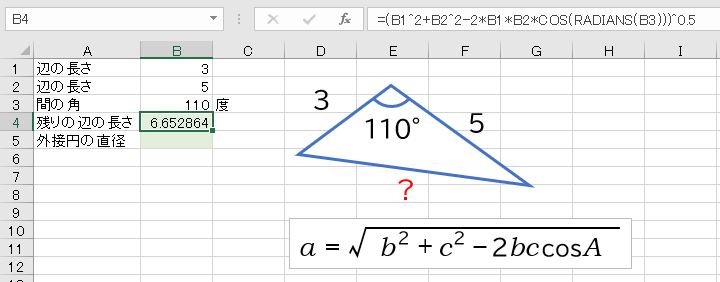
2辺の長さが3と5で、その間の角が110度の三角形について、残りの辺の長さを求めなさい。また、この三角形に外接する円の直径を求めなさい。

解説
直角三角形でない場合は余弦定理や正弦定理等の三角関数の公式を使います。2つの辺とその間の角が分かっている場合は、余弦定理によって残りの辺の長さを求めることができます。
- =(B1^2+B2^2-2*B1*B2*COS(RADIANS(B3)))^0.5
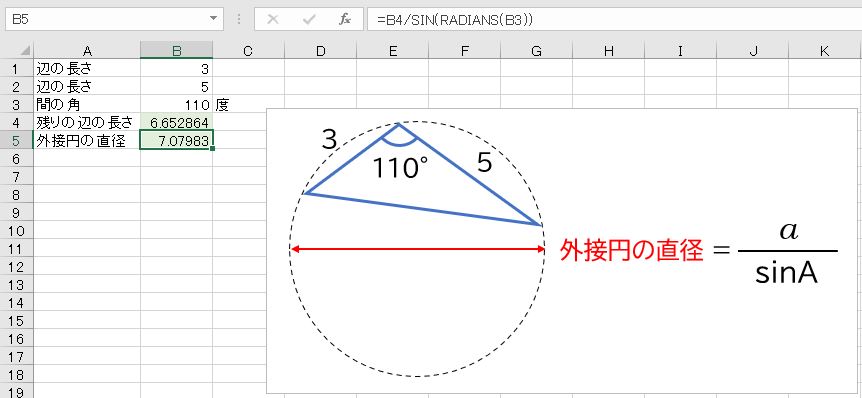
また、向かい合う辺の長さと角が分かれば、正弦定理によって外接円の直径を求めることができます。
- =B4/SIN(RADIANS(B3))
(4)正確でないことがあるので注意
問題
Excelで、sin(180度)とtan(90度)を求めなさい。また、なぜこのような結果になるのかを考えなさい。
解説
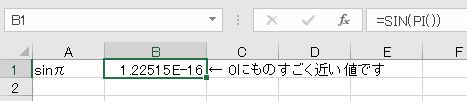
単位円では、0度と180度のときにy座標が0になります。つまり、sin(180度)=sin(π)は0になるはずです。
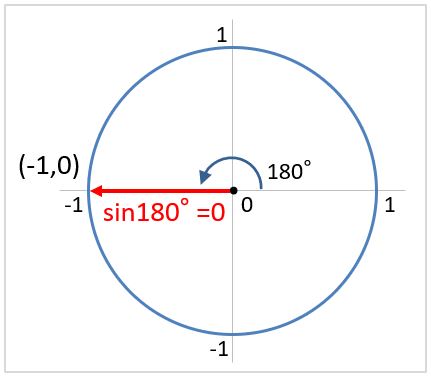
しかし、ExcelでSIN(PI())を求めると0にはなりません(参考:【Excel】なぜ指数の表示形式「E」が表示されるのか、「E」の設定と解除の方法)。
また、90度のタンジェントは定義することができません。90度のときx座標が0になり、0で割り算をすることができないからです。
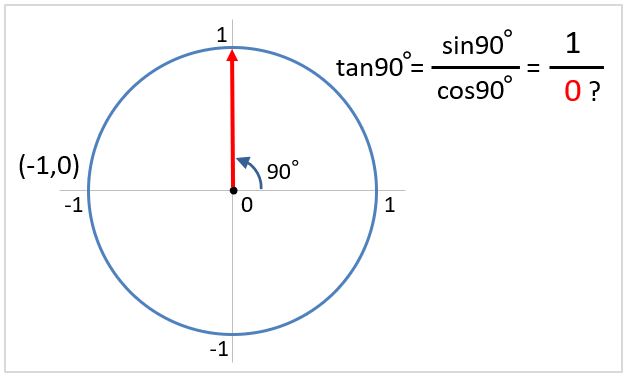
しかし、Excelでtan(π/2)を計算するとエラーになりません。
- =TAN(PI()/2)

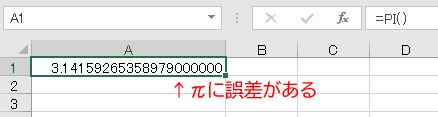
これは、前述のように、円周率PI()が小数第14位までの小数で計算されているためで、正しい円周率よりわずかに小さいことが原因です。また、三角関数の値も小数第14位までの小数で計算されます。このように、三角関数の答えが正しくないことがありますので、注意が必要です。
3.逆三角関数
逆三角関数は、三角関数の逆関数です。通常の三角関数は、角度(ラジアン)から、余弦、正弦、正接を求めますが、逆三角関数はその逆関数なので、余弦、正弦、正接からラジアンを求める関数です。
cos、sin、tanの逆関数はそれぞれarccos、arcsin、arctanです。cos−1 x , sin−1 x , tan−1 x と表記することもあります。
(1)ACOS関数
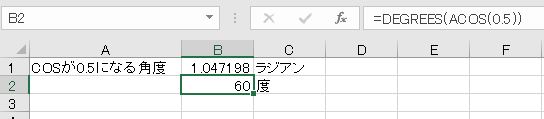
arccos(アークコサイン、逆余弦)は、cosの逆関数です。例えば、π/3ラジアン(60度)の場合、cos(π/3) = 0.5なので、arccos(0.5) = π/3となります。

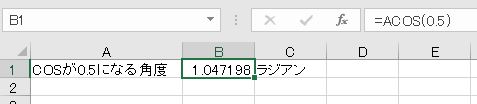
Excelで、arccosを求める関数はACOS関数です。cosの値を-1以上1以下で指定すると、0~πの間の角度(ラジアン)が表示されます。
- =ACOS(0.5)
この値はラジアンなので、度単位にするにはDEGREES関数を使用するか、180/πを掛けます。
- =DEGREES(ACOS(0.5))
- =ACOS(0.5)*180/PI()
cosの値は必ず-1以上1以下なので、-1以上1以下でない値を指定するとエラーになります。
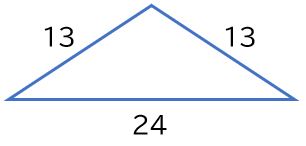
練習問題
等辺=13、底辺=24の二等辺三角形の3つの角の大きさを求めなさい。
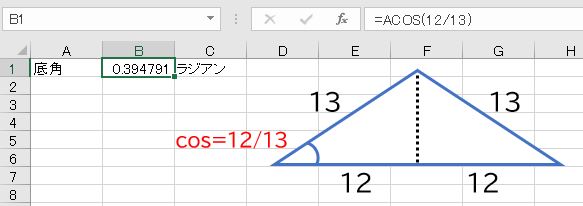
解説
三角比の定義から、底角のcosは12/13です。cosの値が分かっている場合にその角度を求めるには、逆関数であるACOS関数を使います。
- =ACOS(12/13)
ただし、この答えはラジアンなので角度にするにはDEGREES関数を使うか、180/PI()を掛けます。
- =DEGREES(ACOS(12/13))
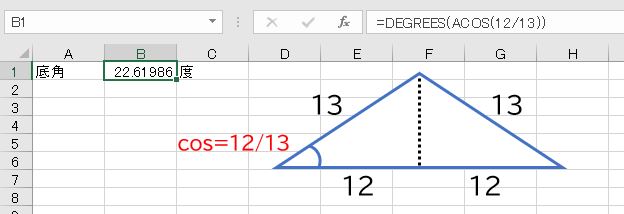
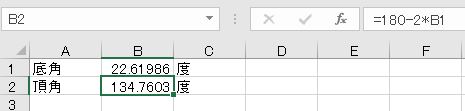
頂角は、2倍して180度から引けばよいです。
(2)ASIN関数
arcsin(アークサイン、逆正弦)は、sinの逆関数です。例えば、π/6ラジアン(30度)の場合、sin(π/6) = 0.5なので、arcsin(0.5) = π/6となります。
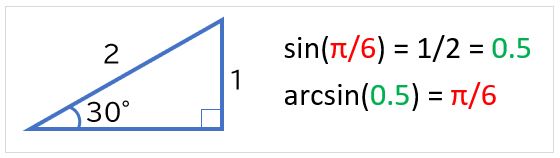
Excelで、arcsinを求める関数はASIN関数です。sinの値を-1以上1以下で指定すると、-π/2~π/2の間の角度(ラジアン)が表示されます。
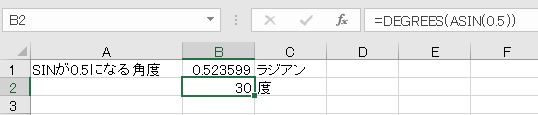
- =ASIN(0.5)
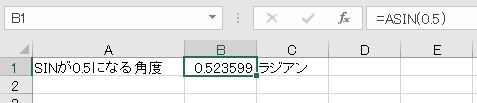
この値はラジアンなので、度単位にするにはDEGREES関数を使用するか、180/πを掛けます。
- =DEGREES(ASIN(0.5))
- =ASIN(0.5)*180/PI()
SINの値は必ず-1以上1以下なので、-1以上1以下ではない値を指定するとエラーになります。
(3)ATAN関数
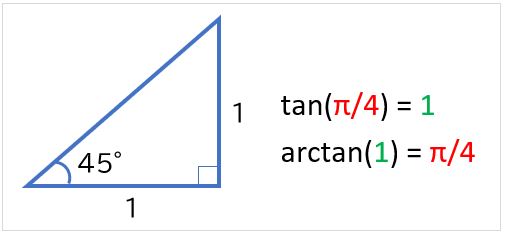
arctan(アークタンジェント、逆正接)は、tanの逆関数です。例えば、π/4ラジアン(45度)の場合、tan(π/4) = 1なので、arctan(1) = π/4となります。
Excelで、arctanを求める関数はATAN関数です。tanの値を指定すると、-π/2~π/2の間の角度(ラジアン)が表示されます。
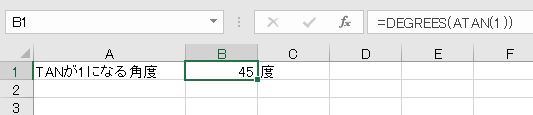
- =ATAN(1)

この値はラジアンなので、度単位にするにはDEGREES関数を使用するか、180/πを掛けます。
- =DEGREES(ATAN(1))
- =ATAN(1)*180/PI()
練習問題
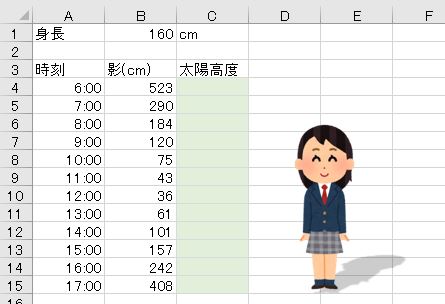
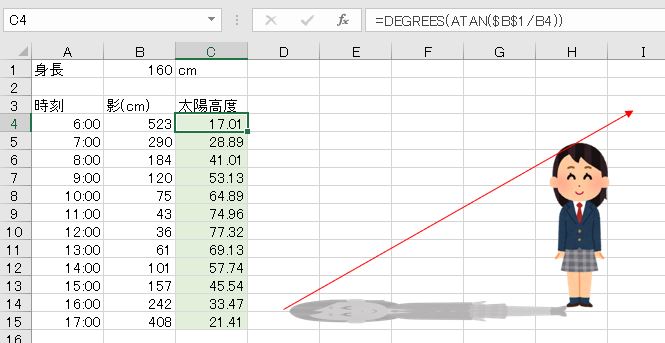
身長160cmの人が1時間おきに影の長さを測った。太陽高度を求めなさい。
解説
タンジェントは傾きを表します。三角比の定義により、影の長さと身長から太陽高度のタンジェントを求めることができます。
- tan(太陽高度)=身長/影の長さ
その角度はATAN関数で求めます。
- =DEGREES(ATAN($B$1/B4))
(4)ATAN2関数
問題
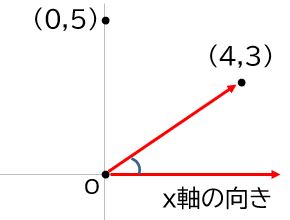
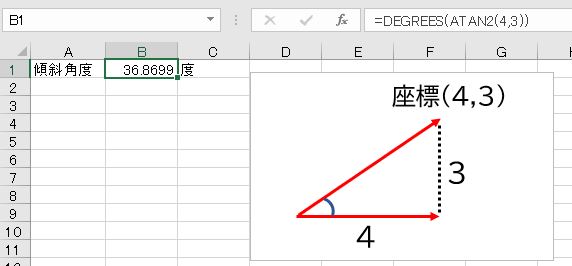
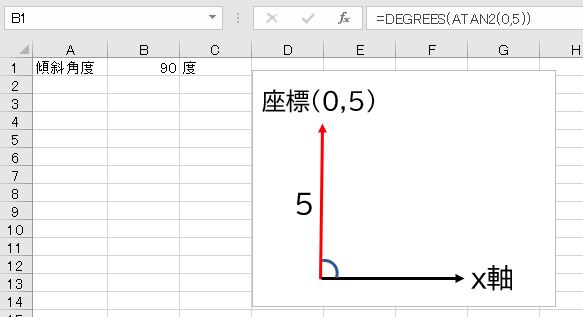
座標軸の原点Oと点(4,3)を結ぶ線は、水平方向(x軸方向)に対して何度傾いているか。また、点(0,5)の場合はどうか。
解説
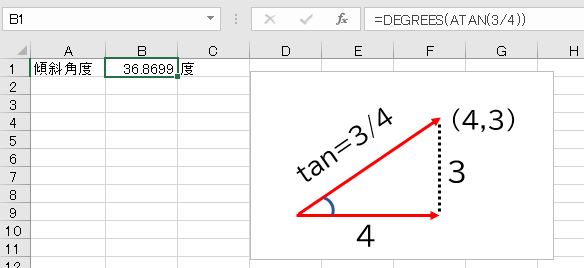
タンジェントは座標軸上の直線の傾きとして考えることもできます。例えば、座標軸の原点Oと点(4,3)を結ぶ線の傾きは3/4ですが、この線の作る角度のタンジェントも3/4です。したがって、逆関数であるarctan(3/4)で角度を求めることができます。
- =DEGREES(ATAN(3/4))
ところで、ATAN関数を使う代わりに、ATAN2関数を使う方法もあります。ATAN2は座標を指定することで角度を求める関数です。
- =DEGREES(ATAN2(4,3))
ATANとATAN2の違いは90度の場合です。y軸上の点(0,5)でATANを使うとゼロ除算のエラー#DIV/0!になります。前述のようにtan(90度)が存在しないからです。
- =DEGREES(ATAN(5/0))

ところが、ATAN2の場合は座標を指定するので90度を求めることができます。
- =DEGREES(ATAN2(0,5))
練習問題
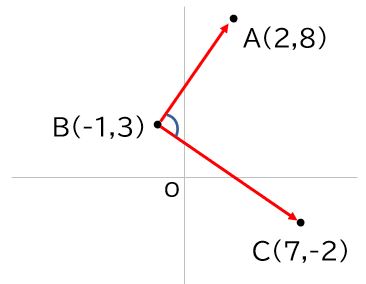
xy座標上の3点A(2,8)、B(-1,3)、C(7,-2)を結んで三角形を作るとき、角Bの大きさは約何度か。
解説
(+1,-3)だけ平行移動すれば、3点の座標は(3,5)、(0,0)、(8,-5)となります。
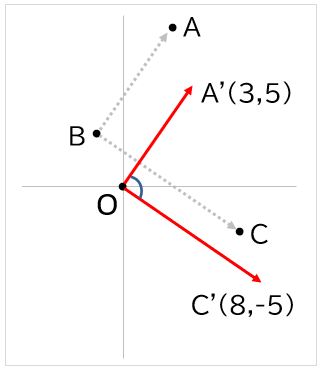
(3,5)、(8,-5)についてATAN2を求めます。
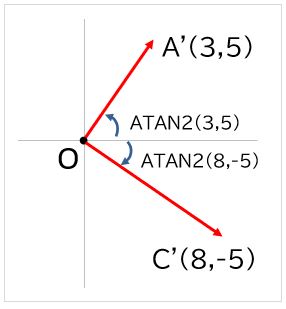
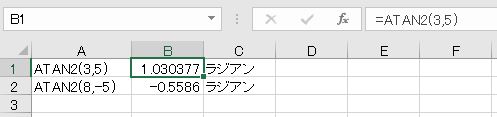
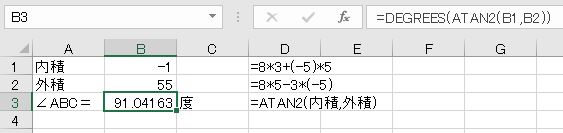
これはラジアンなので角度に直すと約91度であることが分かります。
- =DEGREES(ATAN2(3,5)-ATAN2(8,-5))

<補足>ベクトルを使う方法もありますが、ここでは省略します。
4.割三角関数
割三角関数(かつさんかくかんすう)は三角関数の逆数です。逆数は、掛けて1になる数です(参考:【Excel】逆数と反数、平方根、累乗は初心者の段階で習得すべき_数式の基本)。逆関数ではないことに注意します。逆数を分数で書くのが面倒だからという理由で用意されている関数です。
(1)SEC関数
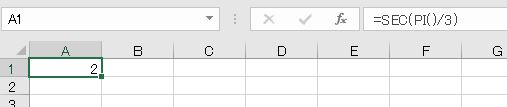
sec(セカント、正割)はcosの逆数です。例えば、π/3ラジアン(60度)の場合、cos(π/3) = 0.5なので、sec(π/3) = 1/0.5 = 2となります。Excelで、secを求める関数はSEC関数です。
- =SEC(PI()/3)
- =SEC(RADIANS(60))
(2)CSC関数
cosec(コセカント、余割)はsinの逆数です。例えば、π/6ラジアン(30度)の場合、sin(π/6) = 0.5なので、cosec(π/6) = 1/0.5 = 2となります。Excelで、cosecを求める関数はCSC関数です。
- =CSC(PI()/6)
- =CSC(RADIANS(30))
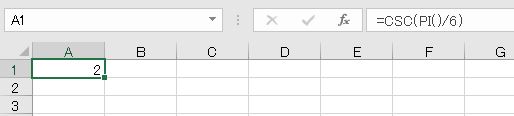
なお、角度が0の場合、sin=0になるため、CSCはゼロ除算#DIV/0!のエラーとなります。
- =CSC(0)

(3)COT関数
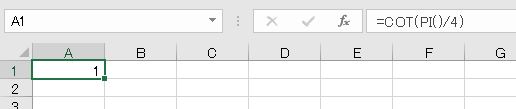
cot(コタンジェント、余接)はtanの逆数です。例えば、π/4ラジアン(45度)の場合、tan(π/4) = 1なので、cot(π/4) = 1/1 = 1となります。Excelで、cotを求める関数はCOT関数です。
- =COT(PI()/4)
- =COT(RADIANS(45))
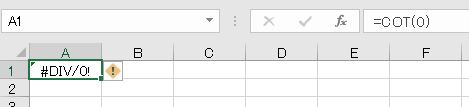
なお、角度が0の場合、tan=0になるため、COTはゼロ除算#DIV/0!のエラーとなります。
- =COT(0)
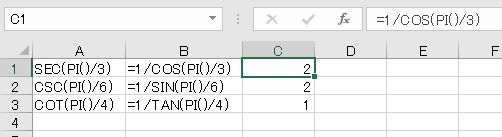
(4)逆数で求めることもできる
SEC関数、CSC関数、COT関数はExcel2013以降に搭載された新しい関数なので、それより前のバージョンで使うことはできません。COS、SIN、TANの逆数で求められますので問題はないでしょう。
- =1/COS(PI()/3)
- =1/SIN(PI()/6)
- =1/TAN(PI()/4)
(5)割三角関数の逆関数
SEC、CSC、COTには、それぞれASEC(アークセカント)、ACSC(アークコセカント)、ACOT(アークコタンジェント)という逆関数が存在し、Excel2013以降で使用することができます。SEC、CSC、COTの値が分かっているときの角度(ラジアン)を求めるもので、使い方はACOS、ASIN、ATANと同じです。
解説は以上です。
