三角比には、sin(サイン)、cos(コサイン)、tan(タンジェント)があり、これらは直角三角形の3辺の長さの比率を表しています。
三角関数は、三角比の考え方を応用して、「原点Oを中心として半径が1の円」の円周上にある点のX座標をcos、Y座標をsinと定義しています。Excelには、三角関数を計算するSIN関数、COS関数、TAN関数がありますが、三角関数の概念が分からなければ使うことができません。
そこで、今回は、三角関数の考え方、SIN関数、COS関数、TAN関数の具体的な使い方と注意点について出題します。
目次
- 0.他の記事のご紹介
- 1.円周率
- 2.COS関数(コサイン)
- 3.RADIANS関数(ラジアン)
- 4.SIN関数(サイン)
- 5.TAN関数(タンジェント)
- 6.三角比の基本問題
- 7.単位円
- 8.散布図で三角関数のグラフを描く
- 9.散布図で回転と移動を考える
- 10.繰り返しの数列を作る
- 11.SIN(PI())やCOS(PI()/2)がゼロにならない問題
- 12.発展問題:角度を求める
0.他の記事のご紹介
三平方の定理と直角三角形の説明についてはこちらの記事をご覧ください。
逆三角関数についてはこちらの記事をご覧ください。
1.円周率
問題
Excelで、半径が1の円の円周の長さを求めなさい。また、半円の場合はどうか。

解説
円周の長さ(円の周りの長さ)は直径に円周率を掛けて求めます。円周率は「PI()」と入力します。半径が1のとき、直径は2なので「=2*PI()」と入力します。

6.28になります。これを2で割ると半円の長さになります。3.14になります。円周率を2倍してから、2で割っているので円周率そのものになります。

2.COS関数(コサイン)
問題
Excelでcos60°(コサイン60度)を求めなさい。
解説
コサインは直角三角形の横の長さ(幅)を斜辺の長さで割ったものですが、これを縮小して斜辺の長さを1にすると、横幅がコサインになります。

60度の三角定規を左右に並べたら正三角形になるので、横幅は0.5(半分)になるはずです。

Excelで「=COS(60)」と入力します。残念ながら0.5にはなりません。

ExcelのCOS関数の角度の単位は、「度」ではなく「ラジアン(radian)」です。したがって、60と入力しても単位が違うので正しい答えにはなりません。

ラジアンとは、180度を円周率のPI()で表す記法のことで、半径=1の半円の弧の長さが円周率と一致することに由来しています(正確には弧度法という)。

180度がPI()なので、60度は3分の1で、「PI()/3」です。

したがって、「=COS(PI()/3)」と入力します。これで、0.5になります。

3.RADIANS関数(ラジアン)
問題
RADIANS関数をもちいてcos60°を求めなさい。
解説
普通の角度をラジアンに換算するには、180度で割ってPI()を掛けます。したがって、60度の場合は「60/180*PI()」、つまり「PI()/3」となります。

ラジアンの換算はRADIANS関数を使うと便利です。角度をRADIANS()で囲みます。

「=COS(RADIANS(60))」と入力します。通常の角度をRADIANS関数で囲むことによって単位がラジアンになります。0.5になります。

4.SIN関数(サイン)
問題
Excelでsin30°(サイン30度)を計算しなさい。
解説
サインは直角三角形の縦の長さ(高さ)を斜辺の長さで割ったものですが、これを縮小して斜辺の長さを1にすると、高さがサインになります。

30度の三角定規を上下に並べたら正三角形になるので、高さは0.5(半分)になるはずです。

Excelで「=SIN(RADIANS(30))」と入力します。SIN関数も単位はラジアンです。0.5になります。

5.TAN関数(タンジェント)
問題
50m先にある建物の屋上を見ると、見上げた時の角度(仰角)が55度だったとする。目の高さが1.6mのとき、建物の高さを求めなさい。

解説
タンジェントは直角三角形の縦の長さ(高さ)を横幅で割ったものですが、これを縮小して横幅を1にすると、高さがタンジェントになります。

横幅にtanをかけたら高さが求められます。50mにtan55°をかけて、目の高さである1.6mを足します。

約76mであることが分かります。
- =50*TAN(RADIANS(55))+1.6

6.三角比の基本問題
(1)辺の長さを求める
問題
直径が50の円がある。直径の端から35度の線を引いたときにできる三角形の2辺の長さを求めなさい。

解説
円周上の3点を結ぶ三角形で、そのうちの一辺が直径の場合、この三角形は直角三角形になります(円周角の定理)。
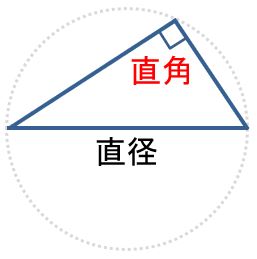
回転してみると、角度が35度で、斜辺が50であることが分かります。
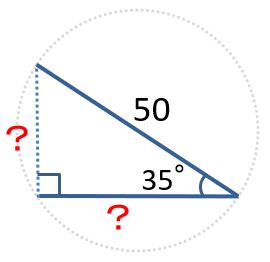
斜辺と角度が分かっている場合、COS・SINで他の辺の長さを求めることができます。
- 直角三角形の横幅=斜辺*COS
- 直角三角形の高さ=斜辺*SIN

直角三角形の幅は、斜辺の長さにCOSを掛ければよいので、「=50*COS(RADIANS(35))」です。

直角三角形の高さは、斜辺の長さにSINを掛ければよいので、「=50*SIN(RADIANS(35))」です。

(2)三角測量と正弦定理
問題
川の同じ側にAとBの地点があり、対岸にC地点がある。三角形ABCで、AとBの距離が100m、角A=30度、角B=45度であることが分かっている。AB、ACの長さを求めなさい。また、川の幅を求めなさい。

解説
いっぱんに、三角形の角のサイン(SIN)と向かい合う辺の長さの比率は同じです。これを正弦定理(せいげんていり)といいます。
- a/sinA=b/sinB=c/sinC

この式に当てはめると、「a/sin30°=b/sin45°=100/sin105°」となります。

したがって、sin30°とsin45°をそれぞれ移項することによってa、bを求めることができます。
- a=100/sin105°*sin30°
- b=100/sin105°*sin45°
Excelで計算してみましょう。
- =100/SIN(RADIANS(105))*SIN(RADIANS(30))
- =100/SIN(RADIANS(105))*SIN(RADIANS(45))

川幅は直角三角形の高さにあたるので、斜辺にSINを掛けたら求められます。

斜辺にSIN(RADIANS(30))を掛けます。

(3)三角形の面積
問題
長さが10と15の2本の線に挟まれた角度が55度のとき、三角形の面積を求めなさい。

解説
三角形の面積の公式と言えば「底辺 * 高さ / 2」が有名ですが、2辺の長さとその間の角度が分かっている場合は「a * b * sin / 2」です。それは、さきほどの川幅の問題と同様、sinを掛けると高さを求めることができるからです。
「=10*15*SIN(RADIANS(55))/2」と入力します。これで三角形の面積を求められます。

7.単位円
問題
角度が111°、222°、333°のCOSとSINをそれぞれ求めなさい。

解説
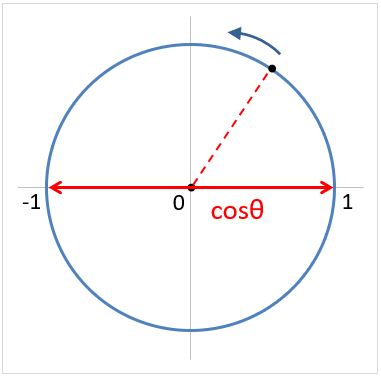
半径が1の円のことを単位円といいます。単位円の中心から斜め上に線を引くとその長さは1です(半径)。

ここで、右方向の直線を0度として、反時計回りに角度をθとします。

COSは斜辺=1の時の直角三角形の幅であり、SINは斜辺=1の時の直角三角形の高さです

したがって、円周上の点の座標は(cosθ, sinθ)です。このことは90度を超えても同じです。

横軸をCOS、縦軸をSINと考えると分かりやすいかもしれません。COSは左に行くほど大きくなり、右半分がプラス、左半分がマイナスです。SINは上に行くほど大きくなり、上半分がプラス、下半分がマイナスです。

111度は左上なので、COSはマイナス、SINはプラスになります。

Excelで「=COS(RADIANS(A2))」「=SIN(RADIANS(A2))」と入力してみましょう。

同様に222°、333°も求めてみましょう。

222度は左下なので、COSもSINもマイナスです。333度は右下なので、COSはプラス
、SINはマイナスになります。

*補足*
ちなみに、測量用語で「方向角」というのがありますが、方向角は北方向(座標では90度方向)から時計回りに計測します。したがって、測量士の計算と、数学やExcelの計算とは反対周りになりますから、注意が必要です。
8.散布図で三角関数のグラフを描く
問題
-360度~+360度までの30度刻みの角度でCOSをもとめ、y=cos(x)のグラフを描きなさい。また、y=sin(x)のグラフを描きなさい。

解説
「=COS(RADIANS(A2))」と入力します。

2列を選択して散布図(平滑線)を選びます。

COSは単位円のx座標なので、360度周期で-1~+1の間を往復します。
「=SIN(RADIANS(A2))」と入力します。

グラフの範囲を広げます。COSとSINは90度横にずれているだけで形は同じです。この曲線のことを「サインカーブ」といいます。

9.散布図で回転と移動を考える
(1)三角関数は回転である
問題
図のように、原点から3の距離にある10個の点を描きなさい。

解説
360度を10等分すると36度です。そこで36度の倍数で360度までの角度を入力します。

cosとsinを求めます。「=COS(RADIANS(A2))」「=SIN(RADIANS(A2))」と入力します。

2列を選択して散布図を描きます。縦と横の高さを同じにします。これで10個の点を描くことができます。

原点を中心にして36度ずつ回転しています。

さらに、3倍します。このように距離をかけることによって、中心からの距離を設定することができます。
- =COS(RADIANS(A1))*3
- =SIN(RADIANS(A1))*3

(2)角度と移動
問題
これら10個の点を、マイナス40度方向に距離10だけ動かしなさい。

解説
マイナス40度とは、時計回りに40度の方向のことです。
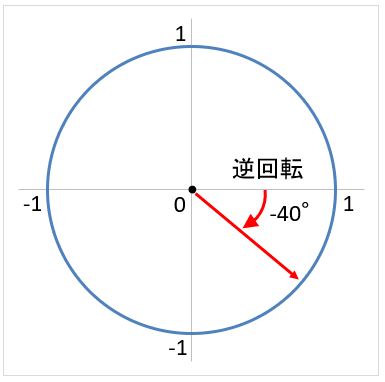
距離が10なので、このx座標は「cos(-40度)*10」、y座標は「sin(-40度)*10」です。これを加算することによって移動させることができます。
- D列:=B2+COS(RADIANS(-40))*10
- E列:=C2+SIN(RADIANS(-40))*10

散布図に別の座標を重ねるには、データの選択をクリックします。

凡例項目(系列)の追加をします。

系列Xの値がCOS(D列)、系列Yの値がSIN(E列)とします。

これで、マイナス40度方向に距離10だけ移動することができます。

10.繰り返しの数列を作る
問題
A列に1~20の整数を入力した。数式を用いて、1、0、-1、0の繰り返しとなる数列を作りなさい。また、A、A、A、B、C、C、C、B、・・・と入力しなさい。

解説
連続データはオートフィルで入力しますが、規則的な数列を数式で作ることがあります(参考:【Excel】計算式で数列を求めることによって規則的にデータを並べる練習 - わえなび ワード&エクセル問題集)。
さきほどの問題でCOSやSINは360度の周期でプラスになったりマイナスになったりします(サインカーブ)。これを利用して、繰り返しの数列を作ることができます。
A列の連番を90倍してSINを求めます。何故か指数表示になります(後述)。
- =SIN(RADIANS(A1*90))

小数点以下を四捨五入すると1、0、-1、0の繰り返しになります。偶数が0で、奇数のうち4で割って1余るものは1、3余るものが-1となります。
- =ROUND(SIN(RADIANS(A1*90)),0)

また、角度を調節することによっていろいろな数列を作ることができます。たとえば、90倍ではなく45倍にすると、1、1、1、0、-1、-1、-1、0、・・・となります。
- =ROUND(SIN(RADIANS(A1*45)),0)

CHOOSE関数で文字に置き換えることもできます。
- =CHOOSE(ROUND(SIN(RADIANS(A29*45)),0)+2,"C","B","A")

11.SIN(PI())やCOS(PI()/2)がゼロにならない問題
問題
Excelを用いてsin180°、cos90°を求めなさい。
解説
「=SIN(RADIANS(180))」を求めます。小数になります。この指数表示「E-16」は小数点の後に0が15個並ぶくらい小さい数で、極めて0に近い数です(参考:【Excel】なぜ指数の表示形式「E」が表示されるのか、「E」の設定と解除の方法)。

しかし、よく考えてみればsin180°というのは単位円上の180°の点のy座標なので0になるはずです。

RADIANS関数の代わりに円周率PI()を使って求めても同じです。
- =SIN(PI())

円周率は無限に続く小数ですが、Excelが計算で用いる有効桁数は15桁なので、小数第14位までの円周率を使って計算します。そのため、ラジアンの計算とそれを用いた三角関数の計算をすると、小数第15位以下の部分で誤差が発生します(これを打ち切り誤差という)。
sin180°は本来ゼロになるはずですが、ゼロになりません。この場合、例えば、小数第15位までの桁数で四捨五入をすればゼロになります。
- =ROUND(SIN(RADIANS(180)),15)
- =ROUND(SIN(PI()),15)

「=COS(RADIANS(90))」を求めます。小数になります。これは「=COS(RADIANS(PI()/2))」としても同じです。

cos90°は単位円上の90°の点のx座標なので0になるはずです。しかし、打切り誤差によってゼロにならないので、四捨五入をする等の工夫が必要です。このように三角関数の計算は円周率を用いているため、誤差が発生します。測量や科学など正確な計算が求められる場合は、Excelを用いて計算してはいけません。

12.発展問題:角度を求める
問題
3辺の長さが3、4、5の直角三角形の4と5の辺に挟まれた角度を求めなさい。

解説
SINは斜辺と高さの比率であり、sin=3/5です。

サインが分かっている時の角度は、ASIN(アーク・サイン)で求めます。「=ASIN(3/5)」と入力します。

この小数の単位はラジアンです。通常の角度に換算するのはDEGREES関数です。「=DEGREES(ASIN(3/5))」とします。だいたい37度くらいであることが分かります。

ちなみにCOSで求める場合、斜辺が1だったら幅は4/5なので、cos=4/5です。

コサインが分かっている時の角度は、ACOS(アーク・コサイン)で求めます。「=DEGREES(ACOS(4/5))」とします。同じ答えになります。

解説は以上です。



