ご存知の方も多いと思いますが、基本情報技術者試験(経済産業省の国家試験)では表計算の問題が出題されます。しかし、出題されている表は訳の分からない使い方をしていて、問題の趣旨を理解するのも一苦労です。この試験の受験対策サイトや合格体験記には「時間の無駄なので後半のマクロは捨てても構わない」などと明言しているものも多数あります。
確かに、業務で、意味不明なExcelファイルを渡されて関数やマクロで処理しなければいけない状況がないとは言えませんが、それを情報処理の国家試験に出題するのは言語道断です。
そこで、今回は、国家試験なのにいろんな意味で表計算ソフトの使い方がおかしい件について、私見を述べたいと思います。そして、最後に問題を用意していますので時間のある人は解いてみてください。
※追記:2019年は良い問題が出題されました。
- 2019春期基本情報技術者試験の表計算をExcel&VBAで完全再現してみた!【表計算マクロ】
- 2019秋期基本情報技術者試験の表計算をExcel&VBAで完全再現してみた!【マクロ】
- 【速報】基本情報技術者試験プログラミング能力、理数能力等に関する出題が強化される【表計算マクロ】
目次
- 0.基本情報表計算・関数シリーズ
- 1.試験の概要
- 2.まずは出題者の愚痴をお聞きください
- 3.C言語選択者が表計算問題を解いてみた
- 4.神Excelワースト3
- 5.表計算問題に多すぎるもの
- 6.表計算問題に足りないもの
- 7.基本情報技術者試験の改善を求める
- 8.表計算問題を作ってみた!
0.基本情報表計算・関数シリーズ
基本情報技術者試験(表計算)の関数とマクロの解説についてはこちらの記事をご覧ください。
- 基本情報技術者試験の表計算に出題される関数一覧とExcelを用いた簡単な練習方法
- 基本情報技術者試験マクロ「相対」の意味を、ExcelのOFFSET関数で理解しよう
- 垂直照合、水平照合、照合検索、表引き、照合一致の関数を自分の言葉で説明しよう
- ExcelのINT関数とMOD関数の使い方で最低限理解しておくべき重要事例
- INT関数とMOD関数をさらに深く理解するための応用の練習問題7題
- 【初心者向け】マクロとは何か?Excel VBA基本の使い方を徹底解説します!動画解説付き
1.試験の概要
基本情報技術者試験は年2回、4月と10月に実施される情報処理の国家試験で、システムエンジニアの多くが受験する有名な試験です。その名の通り、システムを知っている人であれば「基本」的な内容です。
平成21年から試験制度が変わり、平成21年春から表計算、平成23年秋からマクロの問題が出題されるようになりました。アルゴリズムの問題は、C、COBOL Python、Java、アセンブラ、表計算の5つから1つを選択して回答することになっています。
2.まずは出題者の愚痴をお聞きください
(1)採点講評
試験が実施された約2か月後に採点講評が公式サイトに掲載されます。
IPA 独立行政法人 情報処理推進機構:過去問題
https://www.jitec.ipa.go.jp/1_04hanni_sukiru/_index_mondai.html
そのうち、表計算の後半に出題されるマクロの採点講評を抜き出してみました。
- 平成30秋 正答率は低く,あまり理解されていなかった。
- 平成30春 正答率は低く,あまり理解されていなかった。
- 平成29秋 正答率は低く,あまり理解されていなかった。
- 平成29春 正答率は低く,あまり理解されていなかった。
- 平成28秋 d~fの正答率はいずれも低く,あまり理解されていなかった。
- 平成28春 e~gの正答率は低く,あまり理解されていなかった。
- 平成27秋 f,gの正答率は低く,あまり理解されていなかった。
- 平成27春 正答率は平均的で,おおむね理解されていた。
- 平成26秋 正答率は低く,あまり理解されていなかった。
- 平成26春 いずれも正答率は低く,あまり理解されていなかった。
- 平成25秋 e~g の正答率は低く,あまり理解されていなかった。
- 平成25春 d~f の正答率は低く,あまり理解されていなかった。
- 平成24秋 g,h の正答率は低く,あまり理解されていなかった。
- 平成24春 f~h の正答率は低く,あまり理解されていなかった。
- 平成23秋 f,g 及び h の正答率は低く,あまり理解されていなかった。
ほぼ毎回、理解されていません。
唯一、理解されたという平成27年春の問題は、たったの6行でIFの入れ子だけの低レベルな問題だったため、正答率が上がっただけです。どこがマクロなのか?と思うようなクソ問題です。
・ItemRow ← 照合一致(O2, I2~I53, 0)
・UnitRow ← 照合一致(切り捨て(O2, -2), A2~A13, 0)
▲ 論理積([ 解答欄 e ])
|・相対(L1, ItemRow, 0) ← 本日()
|▲ 相対(E1, UnitRow, 0) = null
||・相対(E1, UnitRow, 0) ← [ 解答欄 f ]
|▼
▼
(2)受験生への要望
採点講評には「全体の処理の流れを理解することが重要」「問題設定及び与えられた説明に応じたマクロの作成方法を習得しておいてほしい」などと受験生への要望が書いてあります。毎回、正答率が低いのは受験生の努力不足のせいだと言わんばかりに偉そうな文章が書いてあります。
確かに受験生のレベルの問題かもしれませんが・・・しかし、毎年毎年、理解されない問題を作って悲しくならないのでしょうか?
そして、正答率が低いのは本当に受験生の理解不足のせいなのでしょうか?
3.C言語選択者が表計算問題を解いてみた
実際に受験したときにはCを選択し、今でもCの問題を毎年解いていますが、良い問題が出題されて勉強になります。前半が易しいとか、後半になるほど難しいといったこともなく、すべての設問が平均的な良問です。
それに比べて、表計算が毎回、後半に出題される設問だけが正答率が低いというのはあまりにも不自然です。しかも、出題されているマクロも10~30行程度でそんなに多いわけでもありません。
そこで、平成23年秋から過去15回の表計算の問題を解いてみました。
全部解いてみた結果、理解されない理由がはっきりと分かりました。
問題が難しくて正答率が低いのではなく、出題されている問題の、表計算ソフトの使い方と状況の説明があまりにも下手くそすぎて理解しにくいのです。表も単純化されておらず、神Excelも平気で出題されています。残念ながら良問は1つもありませんでした。
マクロの正答率が低いのは、前半の下手くそな説明文を理解するのに時間がかかりすぎて、後半のマクロは問題文を読む時間がなく適当に答えている(受験界では「捨てる」という)からです。
4.神Excelワースト3
基本情報技術者試験では、長々と仕様を説明しなければ、受験生に理解してもらえない意味不明な表が毎年出題されています。
ここで、近年出題された神Excel問題のなかで特にひどいものを紹介します。
(1)平成28年度秋
建物の改築作業のスケジュールを決定するために、状態遷移の計算をするという理解不能な状況で作られた表です。リフォームの会社が本当にこんな表を作って工期を決めているのでしょうか。
ちなみに、2つ目の表の使い方は、最初にF2:F3に1~20の数値を入力します。マクロを実行すると上の方眼紙の表を用いてH~J列の表が出力され、さらに、別のマクロを実行するとH~J列の表をもとにしてA~C列の表が出力されます。試験時間中にそんな奇怪な使い方を理解しろというのは酷です。

(2)平成29年度春
1つのシートに3つの表を作るなんて試験問題として不適切です。Excelの検定試験でもこんなシートは絶対に出題しません。この表をパッと見て、すぐに使い方が分かる人がいたら天才だと思います。荷物の重量計算をするだけの表です。
もちろん、日本語で使い方の説明が長々と書いてありましたが、なぜこんな複雑な表を作る必要があるのか、何回読んでも全く分かりませんでした。マクロを使用するのであれば、中間の梱包作業表は不要です。上と下の表は合体して1つの表にしてしまえばいいです。

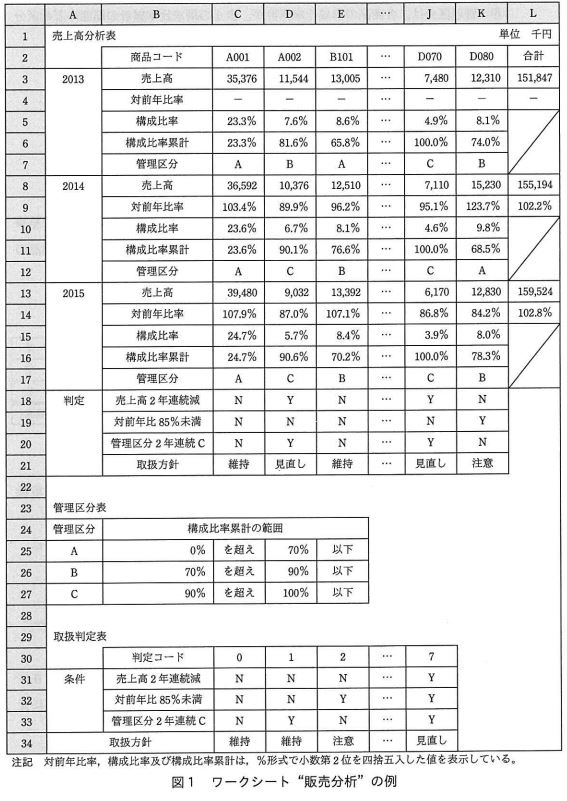
(3)平成28年度春
これは典型的な神Excelです。卸売業者が商品コードを横に並べて分析するという非現実的な表です。出力のための表と判定基準を1つのシートにまとめているのも意味不明です。ABC分析をしているようですが、肝心なマクロの問題は、「3行目、8行目、13行目に西暦と売上高を出力する」だけというお粗末な問題でした。
いやいやいや、他にマクロでできることあるでしょ!!とツッコみたくなります。
5.表計算問題に多すぎるもの
(1)説明が長すぎる
表計算の説明文は無駄に長いです。
他の言語(C,Java,COBOL,アセンブラ)では、プログラムを作成する前提条件(状況)を説明するための問題文が1~2ページくらいであるのに対し、表計算は4ページくらいあります。それとは別に、マクロの仕様も1ページくらい割いて説明しています。そのあとの設問に行くまでに試験時間を無駄に消耗している感じです。
平成25年度春期をはじめ、採点講評には何度か「問題文に書いてあるのに・・・」と述べられているものがあります。
(平成25年度春期)
問題文に「セルE24の値がtrueになるまで繰り返す」という記述があるにもかかわらず,この条件を含まない解答を選択しており,アルゴリズム及び疑似言語の基本的な理解の不足が見られる。
はい、意味不明です。どうして、セルE24という中途半端な場所に「true」と表示する必要があるのでしょうか?そんな場所にフラグを立てて、それを終了条件にするなんて、マクロの使い方として完全に間違っています。
(2)表が単純でないから説明が複雑すぎる
なぜ、長い説明が必要なのでしょうか。
神Excelの表は自己満足で作っているので、複雑な表になりがちです。複雑な表を第三者に理解してもらうためには「このセルはこういう意味で」「ここが空白だったらこうなって」「ここがtrueになるまで繰り返して」と複雑な説明をしなければなりません。パッと見て用途が分かるような単純な表であれば、そのような訳の分からない説明をする必要はありません。
問題文に書いてあるのに見落とすというのは、理解不足ではなく出題者のスキルが不足しているからではないでしょうか?
(3)アルゴリズムの説明が書いてある
表計算の問題は、状況を把握するのに時間がかかりすぎて、肝心なアルゴリズムを問う時間が無いという印象です。設問も低レベルで、日本語を疑似言語に翻訳するだけという残念な問題です。例えば、平成26年秋期の問題には次のようなものがありました。
【問題文】
鉄道区間の全区間(起点駅から終点駅まで)の距離の50%以下の距離は区分番号3の距離の範囲に入るようにする。
1.鉄道路線の全区間の50%の距離を求める。
2.区分番号2の新たな上限距離に区分番号3の単位距離の倍数を加えた値で、かつ、1で求めた距離以上となる最小値を、区分番号3の新たな上限距離とする。
この問題文は、要するにExcelのCEILING関数(切り上げ)のことを説明しているのですが、ご丁寧に計算手順を説明しています。情報処理の担当者がCEILINGのアルゴリズムを細かく説明されないと分からないのでしょうか?
アルゴリズムは自分で考えるものであって、他人が説明することではありません。
6.表計算問題に足りないもの
他の言語では頻繁に「プログラムの変更」や「エラー発生時の対応」に関する問題が出題されます。~~に対応するためプログラムを変更した、他者から指摘を受けてプログラムを追加したといった問題がほぼ毎年のように出題されています(最近では平成30年秋のCOBOL、平成30年春のJavaやC言語など)。しかも、そんなに正答率が低いわけでもなく、素直な良問です。
一方、表計算の問題は、訳の分からないExcelファイルの使い方をダラダラと説明したうえで、疑似言語を穴埋めするだけです。
表計算はエンドユーザに最も近く、ユーザからの要望も多いはずです。数式もマクロも1回作れば終わりではなく、状況の変化に応じて修正や例外処理を入れることも多いです。マクロを変更したときの実行結果や、想定していなかった入力への対応に関する問題がなぜ出題されないのでしょうか。
7.基本情報技術者試験の改善を求める
(1)神Excelは絶対に出題するな!
なぜ、表計算の問題は低レベルなのか。
それは、問題で使われている表が神Excelだからです。表をできるだけ単純化して、処理内容が簡単に理解できるように工夫すべきです。そして、処理の説明を1ページ程度に抑え、本来問うべきアルゴリズムの問題を充実させるべきです。
(2)関数の問題を無くして、マクロだけにしろ!
関数の使い方や絶対参照はITパスポート試験のレベルで聞けばよいです。基本情報でExcel関数の使い方を聞くのはレベルが低すぎます。もし、関数の問題を出すのであれば、ユーザー定義関数の問題を出すべきです。関数が自作できないような人に基本情報の合格証書を与えてはいけないと思います。
マクロでもワークシート関数(相対、論理、照合一致など)を使いますから、前半の関数の問題をすべて無くしてしまってもいいと思います。マクロだけにすればもっとスッキリとした問題になるはずです。
8.表計算問題を作ってみた!
資格試験ですから、アルゴリズムが分かっている人には簡単に見えて、理解不足の人には難しく見える問題にすべきです。というわけで、当ブログは「問題集」なので、サンプル問題を作ってみました。
模擬問題(平成25年春COBOL改題)
創立20周年の会社Xでは、創立記念日に勤続年数0~20年のすべての従業員に特別賞与を支給することにした。シート「支給係数」には次の表が入力されており、基本給に、役職と勤続年数によって導出される支給係数をかけ合わせて、100円未満を切り捨てた金額をもって、特別賞与とすることにした。例えば、管理職(役職コード:1)の従業員が入社日から10年以上経過していたら、その特別賞与の支給係数は0.2である。

次の図はシート「従業員リスト」である。A~C列には従業員番号などが入力されており、図では省略しているが途中に空白等は無いものとする。

役職コード(0または1)と勤続年数(整数)を引数、支給係数(小数)を戻り値とする関数keisuを作成した。
- 関数 keisu(x, y)
引数x:役職コード、引数y:勤続年数
設問(1)
従業員の人数がちょうど100人だったとする。セルF2に「=keisu(D2, E2) * (1 - D2)」と入力してF3:F101に複写した。一般職の支給係数の平均値を求める式はどれか。
ア = 合計(F2:F101) / (100 - 合計(D2:D101))
イ = 1 - 合計(F2:F101) / 合計(D2:D101)
ウ = 合計(F2:F101) / (1 - 合計(D2:D101))
エ = 合計(D2:D101) / (100 - 合計(F2:F101))
オ = 1 - 合計(D2:D101) / 合計(F2:F101)
カ = 合計(D2:D101) / (1 - 合計(F2:F101))
設問(2)
次の図は、関数keisuの概要を示したものである。

次の9個の処理をすべて使って完成させたい。①~④のいずれかに入れて完成させる場合、③に当てはまるものはどれか。
- i ← 1
- i ← i + 1
- sw ← 0
- sw ← 1
- skks ← 0
- yaku ← 相対(支給係数!A3, i, 0)
- nen_min ← 相対(支給係数!A3, i, 3)
- nen_max ← 相対(支給係数!A3, i, 4)
- skks ← 相対(支給係数!A3, i, 5)

シート「従業員リスト」の項目名を次のように変更した。

F列には基本給が数値で入力されているものとする。マクロを実行した時に、H~L列に、特別賞与を現金で支給するときに必要となる紙幣または硬貨の枚数を出力したい。
そこで、次の図のようなマクロkinshuをシート「従業員リスト」に格納して実行したが正しい計算結果にならなかった(kinshu_sum[5]は設問(6)で使用する)。

設問(3)
従業員が100人で、そのうち管理職が15人であった場合、マクロkinshuを1回実行すると、関数keisuは通常何回呼び出されると考えられるか。
ア 15回
イ 85回
ウ 100回
エ 115回
オ 425回
カ 500回
設問(4)
マクロkinshuの下線部「特別賞与の金額を求める」について、あてはまる数式として正しいものはどれか。
ア 相対(A1, i, 5) * 切り捨て(keisu(相対(A1, i, 3), 相対(A1, i, 4)), 2)
イ 相対(A1, i, 5) * 切り捨て(keisu(相対(A1, i, 3), 相対(A1, i, 4)), -2)
ウ 切り捨て(相対(A1, i, 5) * keisu(相対(A1, i, 3), 相対(A1, i, 4)), 2)
エ 切り捨て(相対(A1, i, 5) * keisu(相対(A1, i, 3), 相対(A1, i, 4)), -2)
オ 切り捨て(相対(A1, i, 5), 2) * keisu(相対(A1, i, 3), 相対(A1, i, 4))
カ 切り捨て(相対(A1, i, 5), -2) * keisu(相対(A1, i, 3), 相対(A1, i, 4))
設問(5)
マクロkinshuの修正に関する次のア~カの記述の中で最も適当と考えられるものはどれか。
ア 繰り返し処理の条件を「j:1, j<=5, 1」に修正しなければならない。
イ shuruiとmaisuに代入する処理の順序を逆にしなければならない。
ウ 相対(H1, 0, j)と相対(H1, i, j)の位置を逆にしなければならない。
エ maisu > 0を条件とする分岐の処理を追加しなければならない。
オ kingakuを減らす処理を追加しなければならない。
カ 「i = i + 1」は内側の繰り返し処理の中に入れなければならない。
設問(6)
シート「枚数合計」に次の表を入力した。従業員全員に特別賞与を現金で支給するために必要な、各紙幣または硬貨の合計枚数をB2:B6に求めたい。マクロkinshuに繰り返しの処理を追加するとともに、次のP~Uの6つの処理のうち3つを選んで追加する場合、その組み合わせとして正しいものはどれか。

P ・kinshu_sum[ i ] ← 0
Q ・kinshu_sum[ i ] ← 1
R ・kinshu_sum[ j ] ← kinshu_sum[ j ] + maisu
S ・kinshu_sum[ j ] ← kinshu_sum[ j ] + shurui * maisu
T ・相対(枚数合計!B1, i ,0) ← kinshu_sum[ i ]
U ・相対(枚数合計!B2, i ,0) ← kinshu_sum[ i ]
※ただし、P、Q、T、Uの添え字は i でも j でもよい。
ア P、R、T
イ P、R、U
ウ P、S、T
エ P、S、U
オ Q、R、T
カ Q、R、U
キ Q、S、T
ク Q、S、U
ちなみに最後の問題の答えは設問1から順にア、イ、ウ、エ、オ、イです。
— わえなび|Word-Excelの理論を極める最強の問題集 (@waenavi_jp) 2019年1月10日




