10倍、100倍、1000倍もしくは0.1倍、0.01倍、0.001倍というのは小学校の算数で習いますが、これを10の累乗で表す指数法則は高校数学で習います。指数関数や対数関数は、高校の「数学II」の教科書になりますが、たぶんほとんどの人が習ったことすら忘れていると思います。
マイクロソフトの説明によると、LOG10関数は、「10を底とする数値の対数を返します」とのことですが、習った記憶が無い人にとっては「さっぱり分からん??」という感じだと思います。
そこで、Excelで10の累乗とLOG(LOG10)関数を使ったら何ができるのかについて詳しく説明します。

目次
1.まずは基本から
(1)10の累乗
問題
10の5乗から-5乗までを求めなさい。

解説
A列に5から-5までを入力します。「=10^A2」と入力します。これは10の5乗であり、10を5回かけたものです。10*10*10*10*10と書くのが面倒なので数学では「105」、Excelでは「10^5」と書きます。このとき掛け算をした回数(5回)のことを「指数(しすう)」といいます。

答えは10万になります。0が5個付いていることに注意します。このように10の累乗をした時の指数は0の個数と一致します。

下に行くにしたがって、10で割っていくので小さくなっていきます。0乗は「1」となります。10の0乗は1です。10に限らずどんな数でも0乗をすると「1」になります(そういう決まりなのだから覚えるしかない)。0乗は1です。これは暗記することです。

さらに下に行くと、10分の1になっていきますから、小数点の後の0の数が増えていきます。

10^-1は10分の1、10^-2は100分の1、10^-3は1000分の1です。逆数になっています。

グラフにすると左半分はほとんど0です(0に限りなく近い小数)。ここで大事なのは指数は0以下にならないということです。どんなに小さい数になっても10で割ってマイナスになることは無いです。絶対にプラスです。

(2)常用対数
問題
100000から0.00001までの数が、10の何乗にあたるかを求めなさい。

解説
指数を求めるときはLOG関数を使います。「=LOG(A2)」と入力します。

5となります。10を5回かけたら10万になります。

「=LOG(A2,10)」と書くこともありますが、この10は省略することができます。

また、LOG(A2)をLOG10(A2)としてもよいです。同じ意味です。

10の何乗にあたるかを「常用対数(じょうようたいすう)」といいます。「10の累乗の指数部分=常用対数」です。10でなかったら常用対数とは言いません。常用対数はLOG関数を用いて求めることができます。

(3)累乗と対数は逆算の関係にある
問題
LOG(X)=5のとき、Xはいくつか。また、10^X=100000のときXはいくつか。
解説
常用対数が5ということは、10の5乗にあたる数だということです。「=10^5」と入力すればよいです。100000になります。

逆に100000から指数を求めるにはLOGを使って「=LOG(100000)」と入力します。5になります。

このように累乗と対数の計算は逆算の関係にあります。

(4)10の整数乗でない数の常用対数は小数で表す
問題
3500は10の何乗か。また、0.0035は10の何乗か、Excelで計算しなさい。

解説
10を何回かけても3500にはなりませんから、「3500は10の何乗か」という質問自体が意味不明です。しかし、少なくとも、3回かけた1000と4回かけた10000の間であることは分かります。この場合、3と4の間の小数で表します。

Excelで常用対数LOGを求めてみましょう。3500の常用対数を求めると約3.544となります。高校数学の場合は教科書の最後に載っている常用対数表を使ってややこしい計算をして求めますが、Excelの場合は瞬時に計算してくれます。

3500の常用対数が約3.544ということは、10を3.544乗すれば3500になるということですが、10を3.544回かけるというのは非現実的であまり意味が無いことかもしれません。
- 10^3.544=3500
次に0.0035について考えます。これも10で何回割り算しても0.0035という中途半端な数にはなりません。しかし、10^-2である0.01と10^-3である0.001の間にある数であることは分かります。この場合-2と-3の間の小数になります。

0.0035の常用対数を求めると約-2.456となります。10の-2.456乗となります。
- 10^-2.456=0.0035

(5)LOGを使った式の書き方とExcelでの計算の仕方
問題
次の3つの式をそれぞれExcelで計算しなさい。
- 10-0.5
- log10100
- 10log10(106.1+106.2)
解説
10の-0.5乗は「=10^(-0.5)」と入力します。

logの次にある小さい10は、10の累乗の指数(=常用対数)であることを表します。このことを「底(てい)が10である」といいますが、前述のとおり省略できるので今は無視していいです。そのあとの数が元の数(真数という)です。したがって、「=LOG(100)」と入力します。100は10の2乗なので、答えは2です。

logの前にある数字は単なる掛け算です。したがって、「=10*LOG(10^6.1+10^6.2)」となります。

2.常用対数の定番問題
10の3.544乗のように、小数の指数を求めて何の得があるのかという話ですが、まずは、高校の数学IIで扱う常用対数の定番の問題を押さえておきましょう。
(1)整数部分の桁数
問題
A列の数値の常用対数の整数部分(小数点以下切り捨て)を求めなさい。また、この数値にはどのような意味があるか。

解説
常用対数を求めます。「=LOG(A1)」です。すべて小数になります。

INT関数で小数点以下を切り捨てます。「=INT(LOG(A1))」です。3、4、5、6、7となります。

これに1を加えると桁数になります。いっぱんに「常用対数の整数部+1」で桁数を求めることができます。Excelでは「=INT(LOG(数値))+1」です。これは暗記しても良いです。
(2)数値の桁数を求める
問題
1日目に1円、2日目に2円、3日目に4円、4日目に8円と、前日の2倍の金額を貯金していくものとすると、45日目に貯金する額は何桁になるか。

解説
2日目の金額は2の1乗、3日目の金額は2の2乗、4日目の金額は2の3乗・・・となります。ちなみに1日目は2の0乗です(0乗は必ず1)。45日目は2の44乗と考えられます。

常用対数を求めると13.24となります。

さきほどの「常用対数の整数部+1」の法則に従って、整数部分を求めて1を足してみましょう。14となります。
- =INT(LOG(2^44))+1

したがって、2の44乗は14桁の数であることが分かります。ちなみに、2の44乗を計算すると「17592186044416」なので14桁であっています。しかし、このように実際に計算しなくても「常用対数の整数部+1」で14桁であることがすぐに分かります。
(3)LOG乗って何ぞ?
問題
10の「LOG(2)」乗はいくつか。

解説
小数の指数があるということは、「LOG乗」というのもあるということです(訳が分かりませんね~)。では、Excelで計算してみましょう。「=10^LOG(2)」です。

答えは2です。10をLOG(2)乗すると2になります。LOG(2)は小数に換算すると約0.301ですが、もともと、10を何乗したら2になるかというのを常用対数で無理矢理表現したものがLOG(2)なので、10^LOG(2)は2になるのです。

(4)2の累乗
問題
100個の細菌があり、1秒間で2倍に増えることが分かっている。この細菌が1億個を超えるのは約何秒後か。
解説
100個の細菌が1億個になるということは、100万倍になるということです。100万は10の6乗です。

1秒間に2倍になるので、2のn乗が10万を超えるときのnを求めます。

ところで、さきほどの問題で、2=10^LOG(2)でしたが、2は2の1乗です。

したがって、2の累乗を10の累乗に直すには指数をLOG(2)倍すればよく、逆に、10の累乗を2の累乗にするには指数をLOG(2)で割ればよいです(指数法則)。

10の6乗を2の累乗に直すには、6をLOG(2)で割ればよいので、「=6/LOG(2)」を計算します。19.93となるので、答えは約20秒後となります。

3.10の累乗が何の役に立つのか?
(1)大きい数値の一部を取り出す
問題
12桁の数値「202011291635」は2020年11月29日16時35分を表している。西暦の4桁と月日の4桁と時刻の4桁に分離しなさい。

解説
10の累乗を「10^X」という形で表すことにより、数式がすっきりします。数値の左側を取り出すときにはINTを使います(参考:【Excel】INTやMOD関数を用いて数値の一部を取り出す整数問題と関数の過去問(ITパスポート表計算Part3))。
「=INT(A1/10^8)」と入力します。

この「8」は右側の切り落とす8桁のことです。

次に下4桁を取り出すときはMODを使います。「=MOD(A1,10^4)」と入力します。

この「4」は右側の4桁のことです。

途中の4桁は右側の4桁消してから、さらに右側の4桁を残すので「=MOD(INT(A1/10^4),10^4)」となります。

(2)複数回答を1と0で表す
問題
10個の選択肢の中から複数回答することのできる質問をして、A1:D5のような回答を得た。これを1と0の10桁の整数で表しなさい。例えば、1101000000は1番と2番と4番を回答していることを表し、左から数えて回答しているものは1、回答していないものは0とする。

解説
1を回答した場合は一番左を1にするので10の9乗です。2を回答した場合は左から2番目を1にするので10の8乗です。・・・10を回答した場合は10の0乗つまり1です。

つまり、Xを回答した時には10の10-X乗すればよいです。ただし、空白の場合は0にしなければなりません。

IF関数を用いて「=IF(A1<>"",10^(10-A1))」とします。

これを4つ繰り返します。数式が少し長くなりますが、同じものを4回足しているだけです。
- =IF(A1<>"",10^(10-A1))+IF(B1<>"",10^(10-B1))+IF(C1<>"",10^(10-C1))+IF(D1<>"",10^(10-D1))
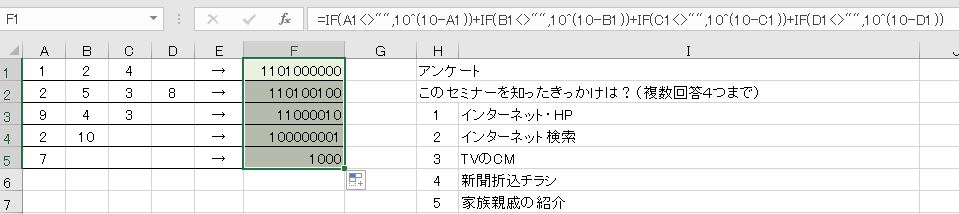
表示形式を「0000000000」にします。

4.常用対数が何の役に立つのか?
(1)上から5桁目以降を0にする
問題
A列の上から5桁目以降を切り捨てて0にしなさい。

また、10000未満の場合に、1の位を切り捨てるにはどうすればよいか。

解説
切り捨てをするときはROUNDDOWN関数を使いますが、桁数の指定は小数点の位置から数えるので、「上から」の位置を指定することができません。
ここで、「=3-INT(LOG(A1))」と入力します。これで切り捨てをする桁数が求められます。上からN桁目を切り捨てる場合の桁数は「N-2-INT(LOG(元の数値))」です。

したがって、「=ROUNDDOWN(A1,3-INT(LOG(A1)))」とすれば、上から5桁目以降が0になります。上からN桁目を切り捨てる場合は、「=ROUNDDOWN(元の数値,N-2-INT(LOG(元の数値)))」となります。

1の位を切り捨てる場合、その桁数の指定は「-1」なので、桁数の上限を-1にすればよいです。上限はMINで設定します(参考:【Excel関数】最大なのに下限のMAX、最小なのに上限のMIN)。
- =ROUNDDOWN(A1,MIN(3-INT(LOG(A1)),-1))

(2)上から2桁目と3桁目を99にする
問題
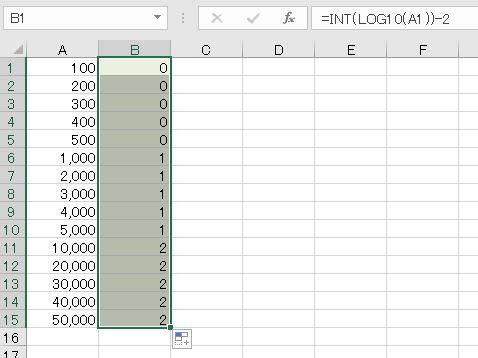
A列に、上から2桁目以降が全て0になっている数値を入力した。B列のように、上から1桁目を1減らして、上から2桁目と3桁目を99にしなさい。

解説
まずはA列からB列を引いてみます。10の累乗になっていることが分かります。しかも、A列の桁数よりC列の桁数のほうが2つ少ないです。

これを踏まえて計算してみましょう。常用対数を整数にして2を引きます。
- =INT(LOG10(A1))-2
これを10の指数にして、元の数から引けばよいです。
- =A1-10^(INT(LOG10(A1))-2)

(3)有効数字3桁にする
問題
A列の数値の上から4桁目を四捨五入して、上から3桁までにしなさい。

また、A列の数値が1000未満の場合に小数点以下を四捨五入するにはどうすればよいか。

解説
四捨五入によって上からの桁数をN桁にすることを有効数字N桁といいますが、有効数字の桁数がN桁の場合、上からN+1桁目を四捨五入しますから、「=ROUND(元の数値,N-1-INT(LOG(元の数値)))」となります。「=ROUND(A1,2-INT(LOG(A1)))」と入力します。

小数点以下を四捨五入するには桁数を0にすればよいのでIF関数を使って強制的に0にすればよいです。
- =ROUND(A1,IF(A1<1000,0,2-INT(LOG(A1))))

(4)3桁ごとの単位
問題
ギガ(G)は10の9乗を表す単位である。この他、メガ(M)、キロ(k)、ミリ(m)、マイクロ(μ)などがあり、10の累乗を表している。A列の数値をこれらの単位で表し、B列の数値が1以上1000未満の数値で有効数字3桁になるようにしなさい。なお、セルF5には「=""」が入力されている。

解説
25000円のことを25Kと表記することがありますが、これは0をたくさん打つのが面倒なので、略して表記するものです。このような単位は1000=10の3乗ごとにあります。
まず、常用対数を求めます。

これを3の倍数で切り捨てます。これによって単位が必要かが分かります。
- =FLOOR(LOG10(A1),3)

10の累乗にして元の数を割れば、1以上1000未満の数になり、整数部分が1桁~3桁になります。
- =A1/10^FLOOR(LOG10(A1),3)

さきほどの問題と同じように、桁数を2-INT(LOG(A1))にして四捨五入すれば有効数字3桁になります。
- =ROUND(A1,2-INT(LOG(A1)))/10^FLOOR(LOG10(A1),3)

単位についてはVLOOKUPで検索します。
- =VLOOKUP(FLOOR(LOG10(A1),3),$E$2:$F$7,2,0)

別解
単位についてはCHOOSE関数を用いる方法もあります。
- =CHOOSE(LOG(A1)/3+3,"μ","m","","k","M","G")

MID関数を用いる方法もあります。詳しくはこちらの記事をご覧ください。
5.科学計算のソフトじゃないので限界はありますよ
なお、Excelは有効桁数の15桁以上の計算ができませんので、天文学的に大きい数や、素粒子物理学のような小さすぎる科学計算はできません。15桁以内の計算でお使いください。
解説は以上です。




