Excelの教科書には、平均はAVERAGE関数で求め、たいていの場合はオートSUMボタンを使えば足りると書いてあります。しかし、AVERAGE関数で求められる平均は「単純な平均(算術平均)」であり、加重平均は求められないということに注意しなければなりません。つまり、平均をする対象の重み(比重)が異なる場合はAVERAGE関数を使ってはいけません。
そこで、今回は、加重平均の意味とExcelで加重平均を計算する方法について出題します。
目次
問題文のあとに簡単な操作方法を解説していますが、静止画では、わかりにくいと思いますので、最後に動画を載せています。ぜひご覧ください。
- 1.加重平均の「重み」とは何か
- 2.単純平均と加重平均
- 3.絶対に平均をたしてはいけない
- 4.データの偏りと加重平均
- 5.平均の平均は加重平均である
- 6.数量が多すぎて分からない場合に数量を推定する方法
- 7.ポイントに換算する(GPA)
- 8.SUMをSUMでわる
- 9.移動平均について
- 10.動画版はこちら(無料)
1.加重平均の「重み」とは何か
問題
Aさん、Bさん、Cさんの財布にはそれぞれ紙幣が10枚、5枚、3枚入っています。3人の「枚数の平均」を求めることは適切といえるか。
解説
(1)平均とは何か
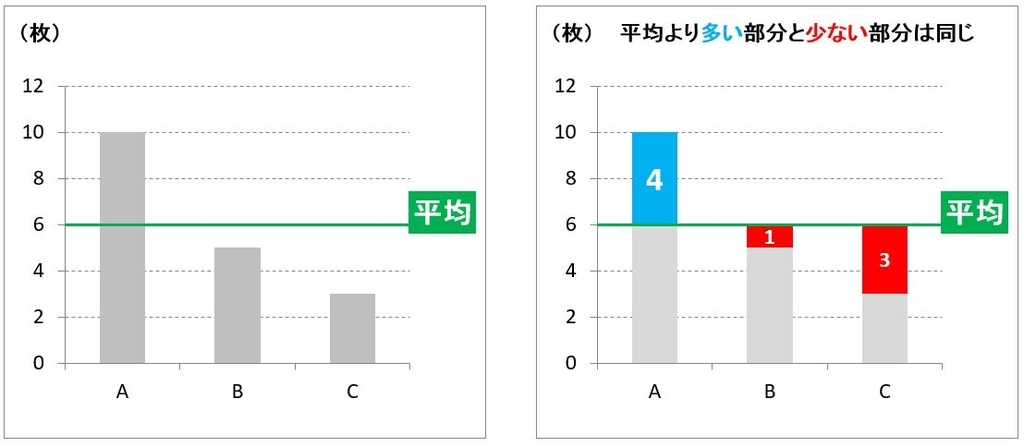
単純に平均を求めるだけであれば、(10+5+3)/3=6となり、平均6枚となります。
いっぱんに、平均を求めると、そのラインより多い部分と少ない部分の合計は同じになります。AさんがBさんに1枚渡し、AさんがCさんに3枚渡せば、3人とも「6枚」となります。つまり、平均とは、超えている部分で、不足している部分をちょうど補うことができるラインを求めているのです。この考え方は、3人の持っている紙幣の価値がすべて同じであれば正しいです。
(2)平均を求める意味があるのか?
しかし、例えば、Aさんの紙幣が千円札で、Bさん、Cさんの紙幣が一万円札だった場合、この大小関係はおかしいです。Aさんのお金で、Bさん、Cさんの足りない部分を補うという考え方も間違いです。
そして、「平均6枚」という答えは何の意味もありません。千円札と万札では1枚の価値が違います。種類が異なるもの同士で不足を補うことはできないので、単純に平均を求めてはいけません。

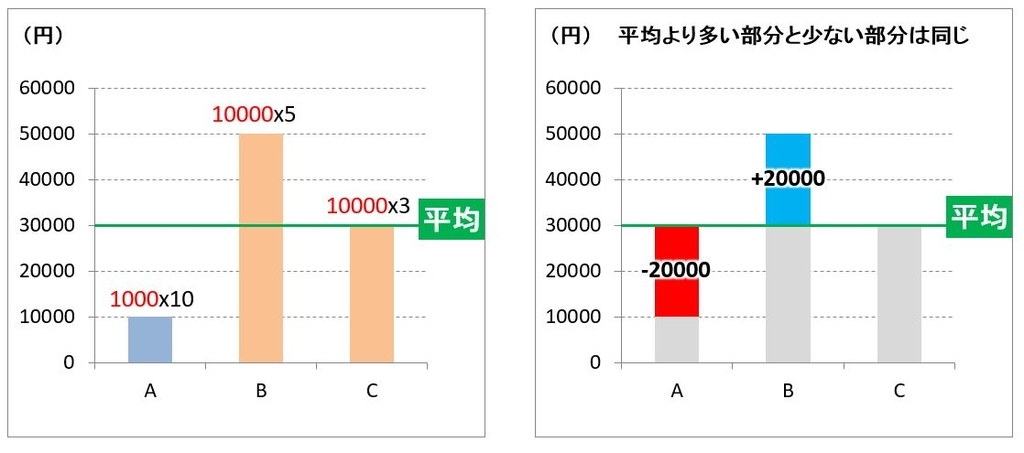
価値が異なる場合はその価値を数値化して、掛け算してから平均を求めます。これを「重み」といいます。
- (1000*10+10000*5+10000*3)/3=平均30000円
2.単純平均と加重平均
問題
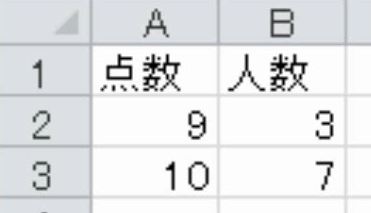
有名人の物まねをしたところ、9点を付けた審査員と10点を付けた審査員がいた。次の表を用いて、平均点を求めなさい。
解説
審査員が2人しかいなくて、9点と10点であれば、9と10を足して2で割って、平均を真ん中の9.5点にすればよいです。

しかし、審査員が10人いて、10点を付けた人が多ければ、100点満点に近くなるわけですから、平均は、真ん中の9.5点より大きくなるはずです。
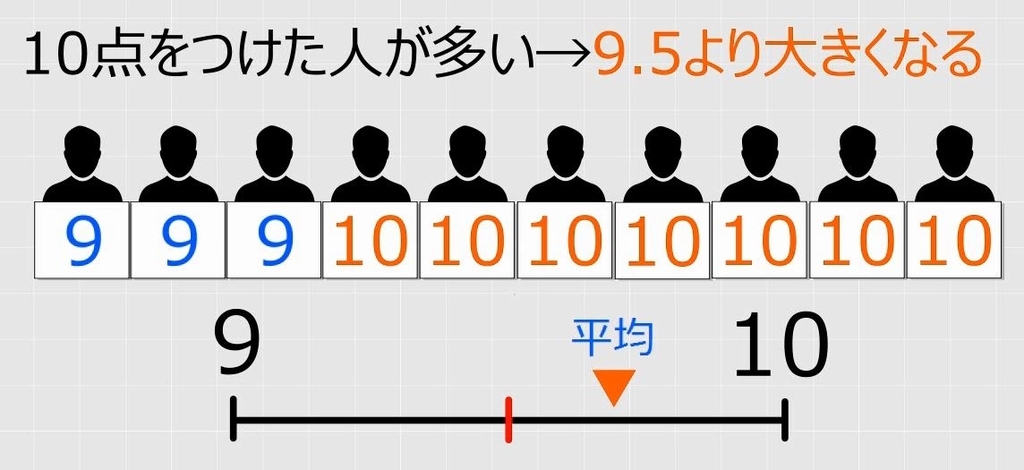
9点と10点の比率によって平均は変わります。10点を付けた人が多ければ10点に近づき、逆に、9点の人が多ければ9点に近づきます。
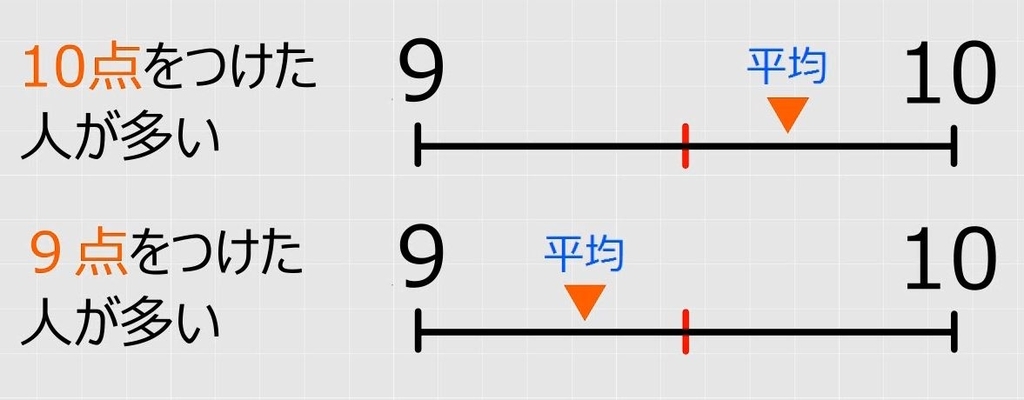
このように、人数や偏りなどの比率を考えない、単純な平均を「単純平均」または算術平均または相加平均といい、比率を考えた平均を「加重平均」といいます。また、このときの比率を「比重(ウェイト)」といいます。


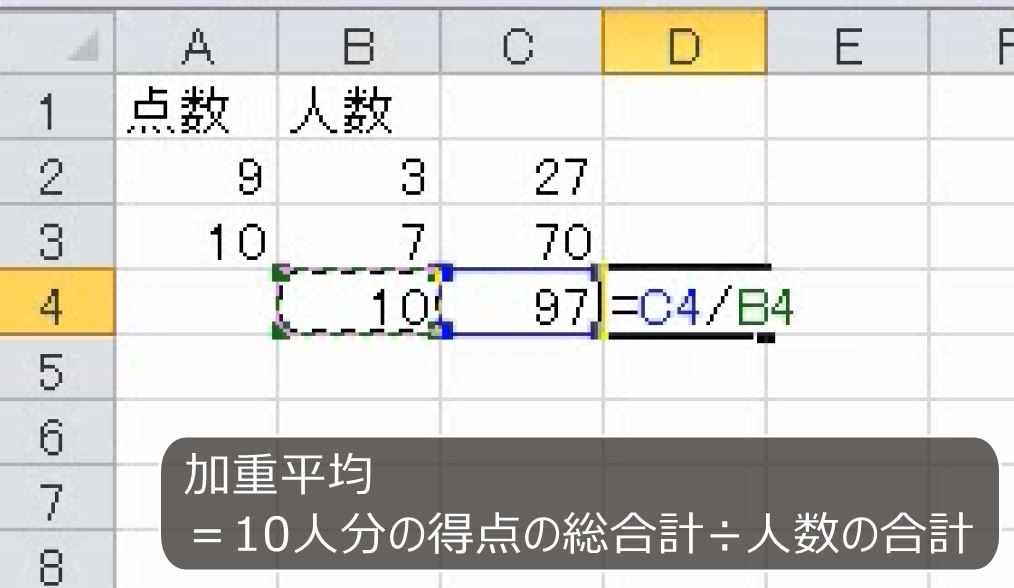
人数をかけて合計点を求めます。合計は97点です。10人で割って9.7点です。
3.絶対に平均をたしてはいけない
問題
次の2つの問題をExcelで計算しなさい。
(1)次の表は7月1日から7月3日に何ページ読書をしたかを表している。3日間で、1日平均何ページ読書をしたか計算しなさい。
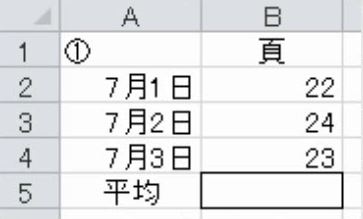
(2)次の表は8月から10月に1日平均何ページ読書をしたかを表している。3か月間で、1日平均何ページ読書をしたか計算しなさい。

解説
3日間のページ数があって、1日当たりの平均を出すのであれば、これは単純平均です。
3つをたして3でわるだけです(AVERAGE関数でもよい)。
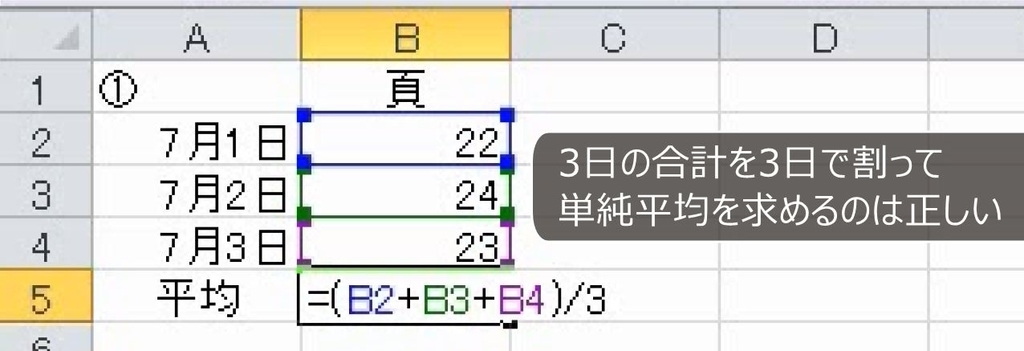
次は、月の平均です。この場合、足して3で割ってはいけません。
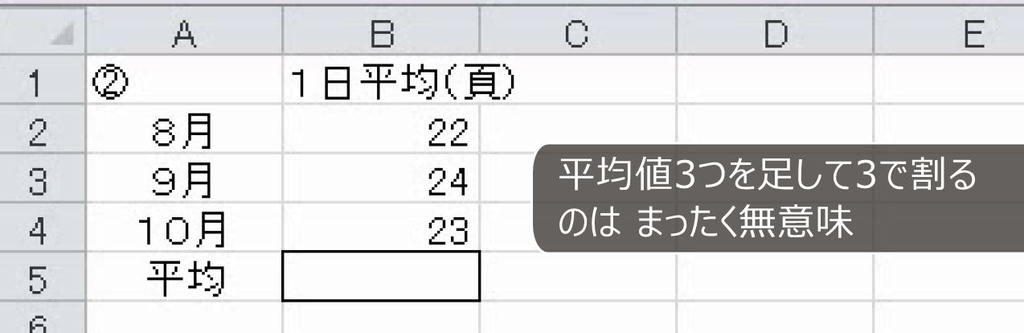
8月は1か月間のページ数を31日で割っています。このように平均にはそれぞれ重みがあります。重みの違う平均値を単純に足したり、さらにその平均を出すような計算をしてはいけません。

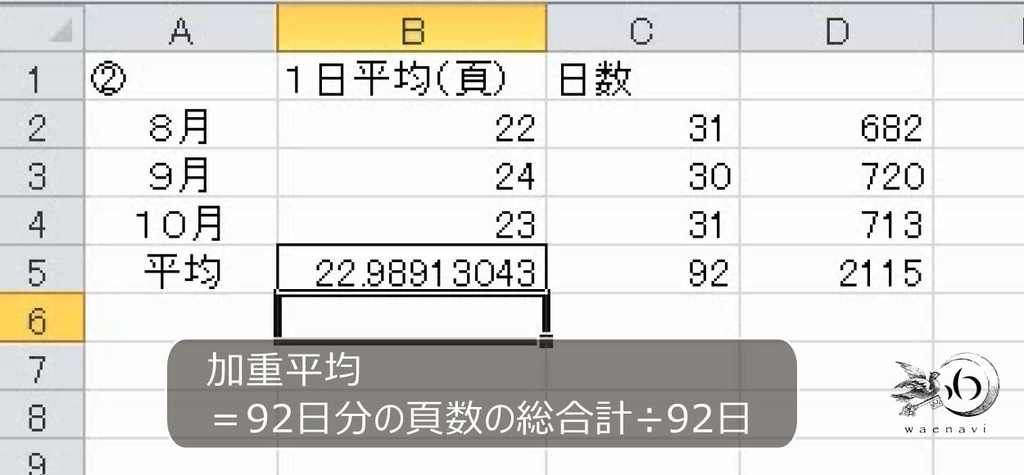
8月と10月は31日、9月は30日しかありません。3か月間で考えると、22ページ、24ページ、23ページの個数が異なります。平均を用いて、さらに平均を求めるときは、比重が異なるので加重平均にしなければなりません。

日数をかけてから計算します。
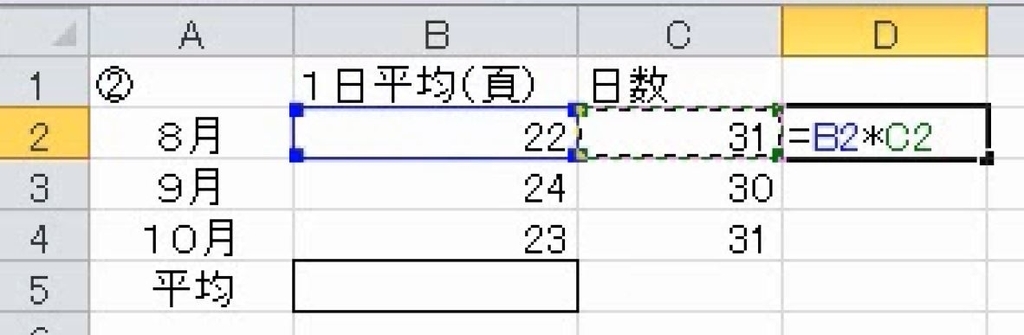
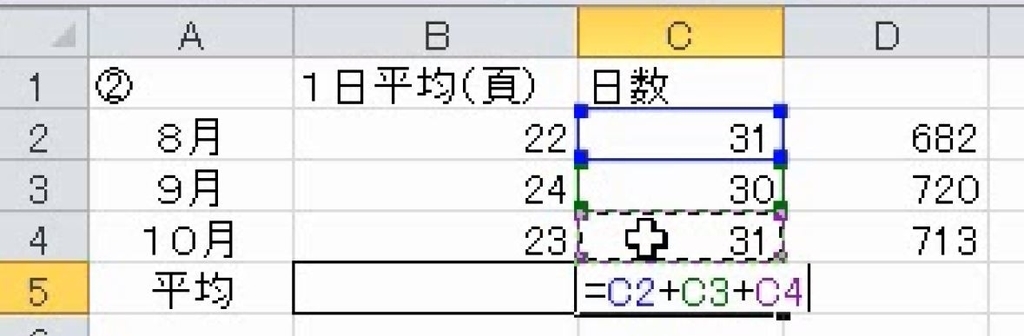
3か月の合計ページ数を、合計日数で割ります。
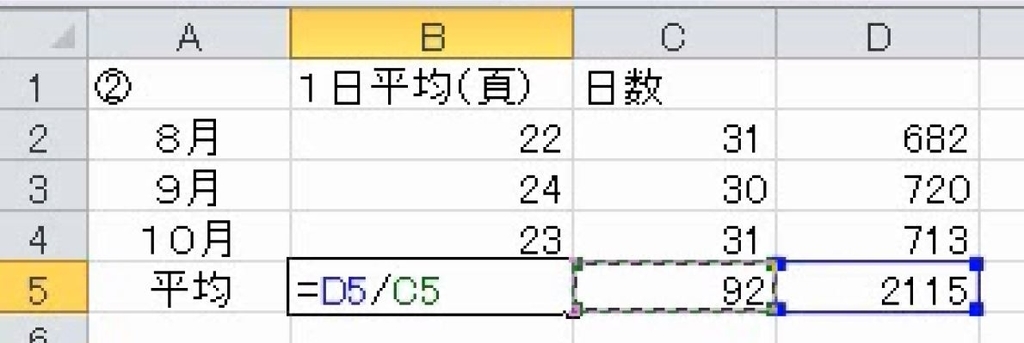
4.データの偏りと加重平均
問題
10人の審査員が10点満点で、9点または10点を付けるとき、次の表を用いて加重平均を求めなさい。

解説
10人の審査員が9点または10点を付けるとき、その人数の組み合わせは、表のとおり11通りあります。加重平均を求めます。9点が10人、10点が0人で合計を求めて10で割ります。A列を固定した複合参照です。

オートフィルをします。これで完成です。10点の人が多くなると平均点は上がっていきます。

5人ずつの場合、9.5点になり、9点と10点の単純平均と同じです。
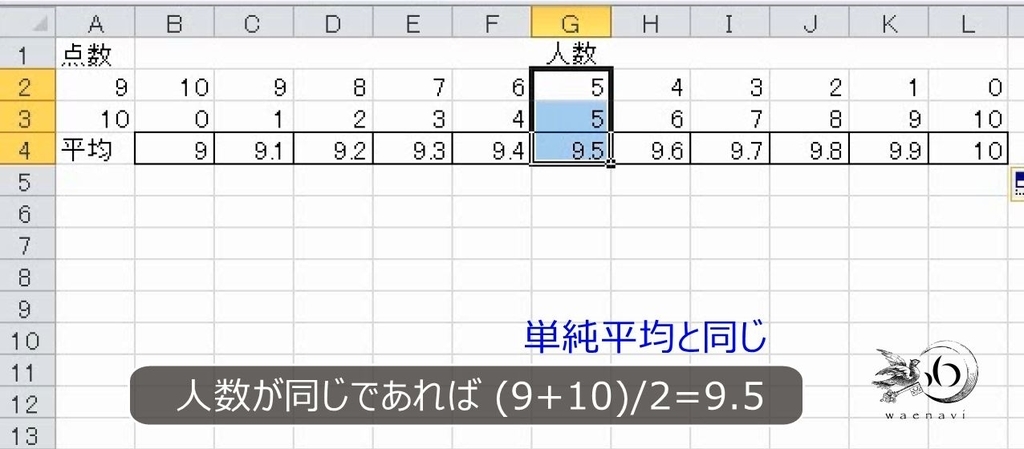
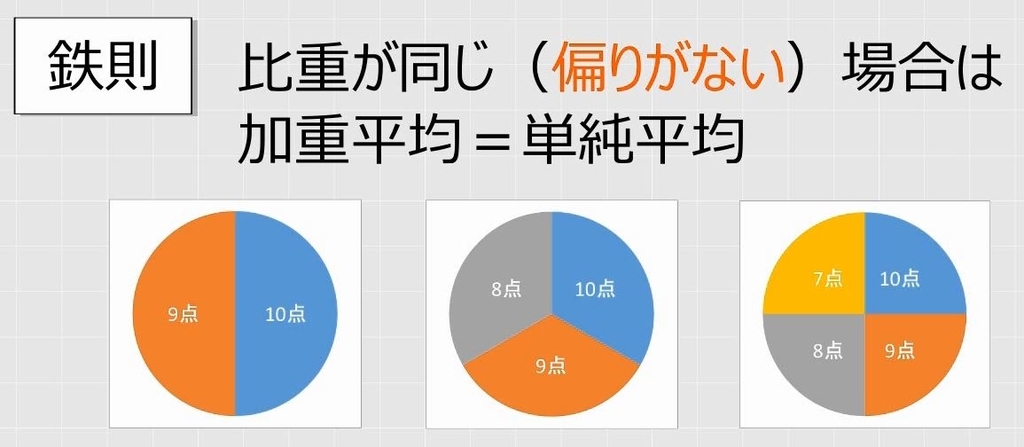
このように比率が同じ、つまり、偏りがない場合は、加重平均と単純平均は同じになります。
5.平均の平均は加重平均である
問題
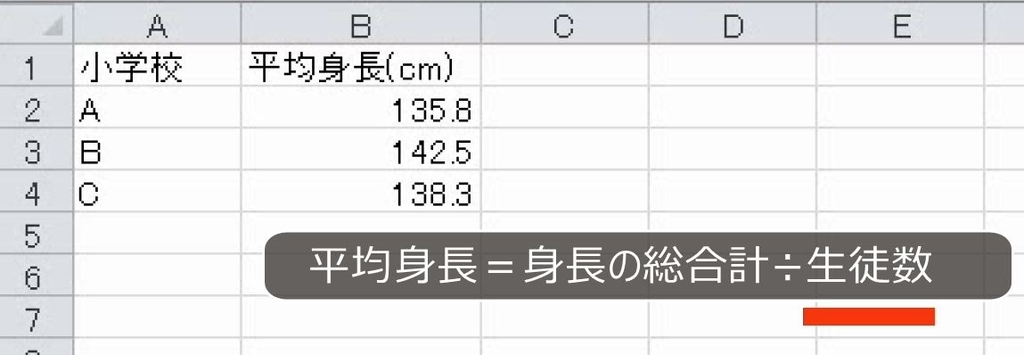
次の表から3つの学校の小学生の平均身長を求めたい。これ以外に必要なデータは何か、述べなさい。また、そのデータがあった場合の計算式を入力しなさい。

解説
いくつかのグループの平均があって、これを合わせた平均を求めるときには、必ず加重平均にします。加重平均はそれぞれのグループの数量が必要です。

ところで各学校の平均値は、それぞれの生徒数で割り算して求めていることは明らかです。したがって、必要なデータは生徒数です。
そこで、例えば、生徒数がこのような場合に加重平均を求めてみましょう。

掛け算をして合計を求めます。生徒数と身長の合計を求めます。
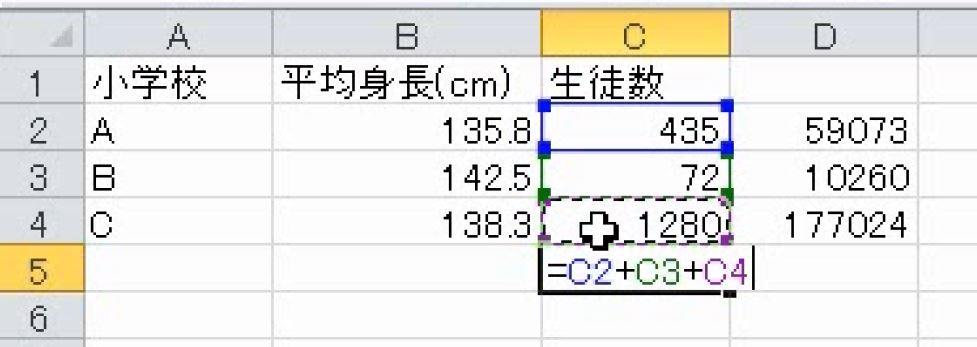
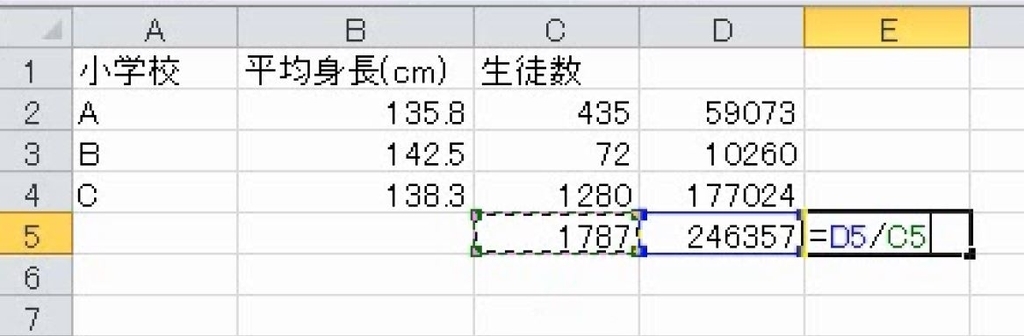
割り算をして平均を求めます。平均137センチです。
6.数量が多すぎて分からない場合に数量を推定する方法
問題
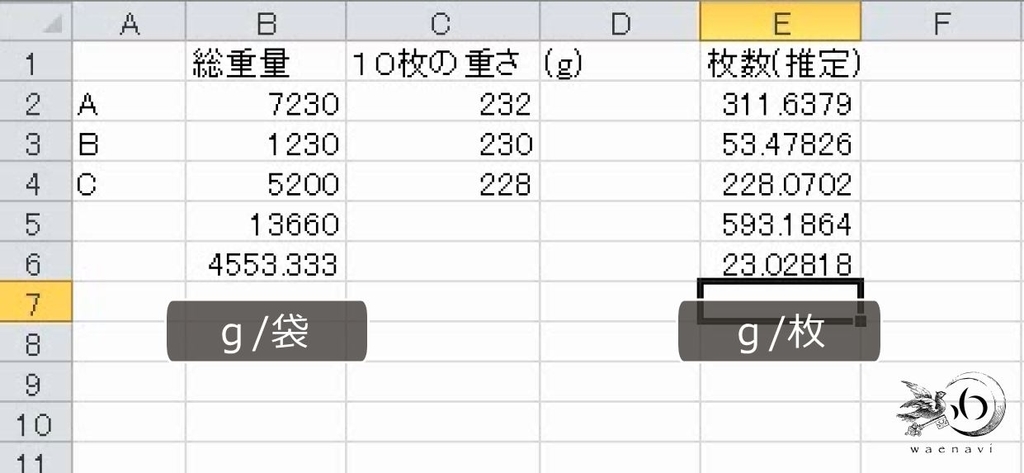
3つの袋A、B、Cにメダルが大量に入っている。袋自体の重さを除く総重量と、袋から10枚取り出したときの重さを計量したら、次のようになった。3つの袋を1つにまとめたとき、メダル1枚の重さは平均何gと考えられるか。
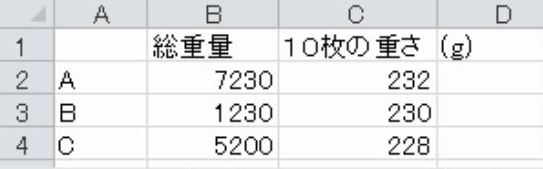
解説
3つの袋の総重量は13660gです。
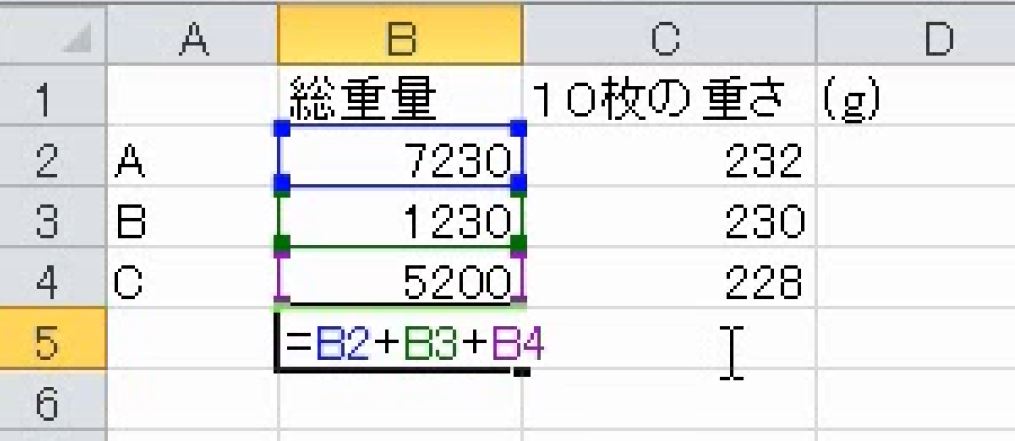
これを3で割ると1袋の平均重量が出ます。単純平均です。
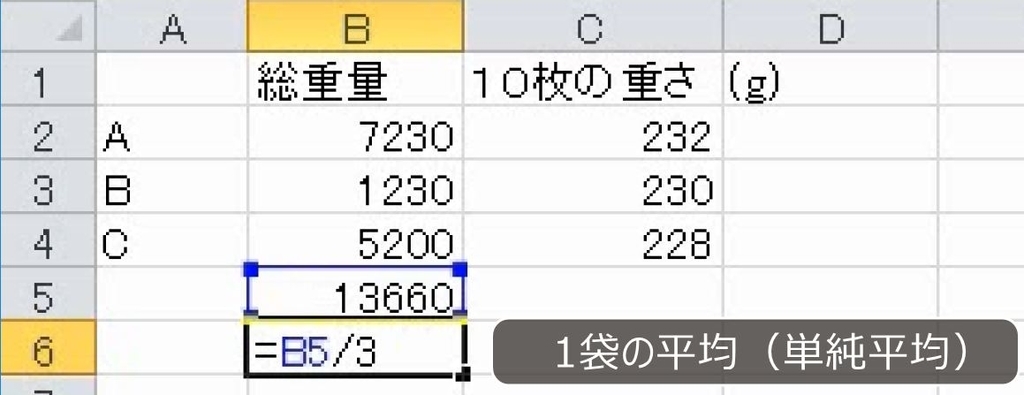
しかし1枚あたりの場合は枚数が必要です。加重平均を求めるには数量が必要です。しかし、数量が多すぎて数えられないときは、一部をサンプルとして抜き出して数量を推定することができます。サンプルの枚数と重さを量って比例計算します(参考:単位の換算と換算倍率、比例計算に関する応用問題)。
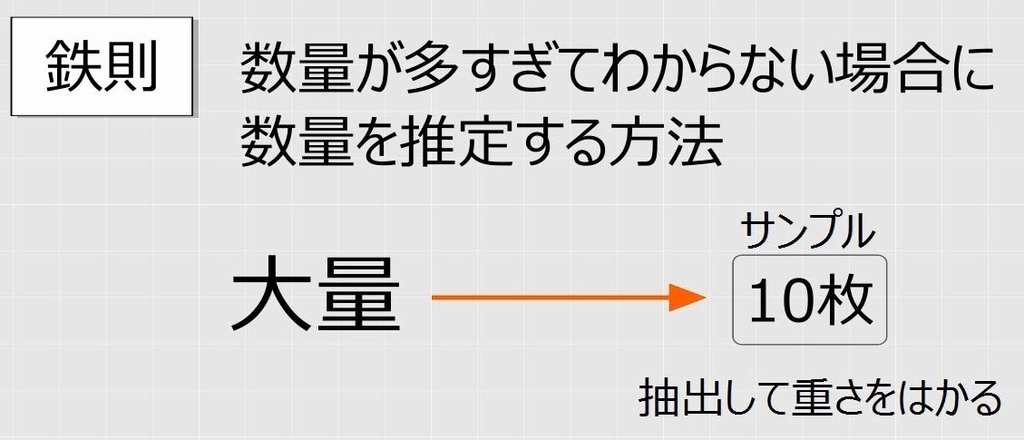
10枚が233gの袋Aが7230gで何枚になるかは、倍率が7230/233でこれを10倍します。
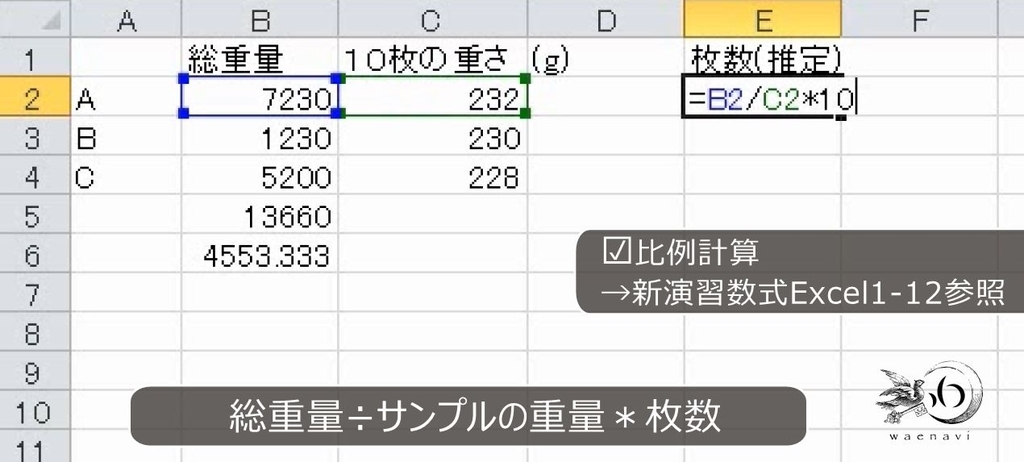
310枚であると考えられます。オートフィルをします。これでそれぞれの枚数が出ます。重量の合計が13660gで、枚数が約590枚です。
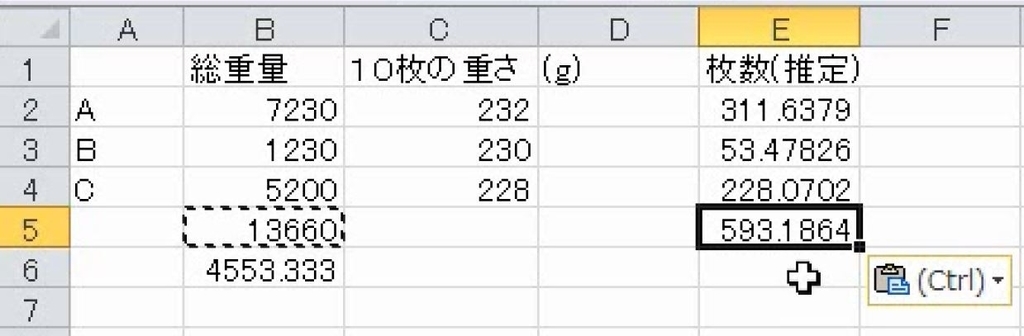
重量を枚数で割ります。これで完成です。1枚平均23.1gとなります。
7.ポイントに換算する(GPA)
問題
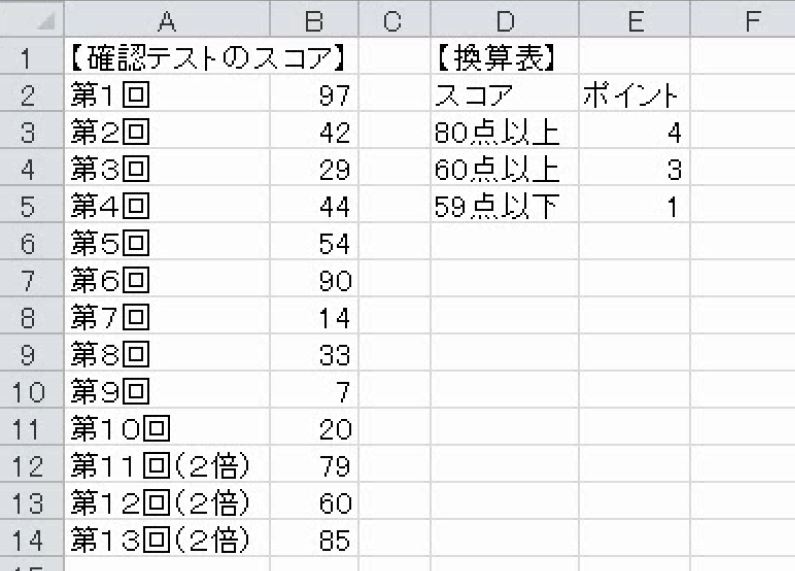
1000点満点の確認テストを13回実施した。このスコアを、換算表に従ってポイントに換算する。
(1)テスト1回あたりの平均ポイント数を求めなさい。
(2)第11回~13回は試験時間が2倍であった。第1回~10回を1単位、第11回から13回を2単位としたとき、単位数あたりの平均ポイント数を求めなさい。
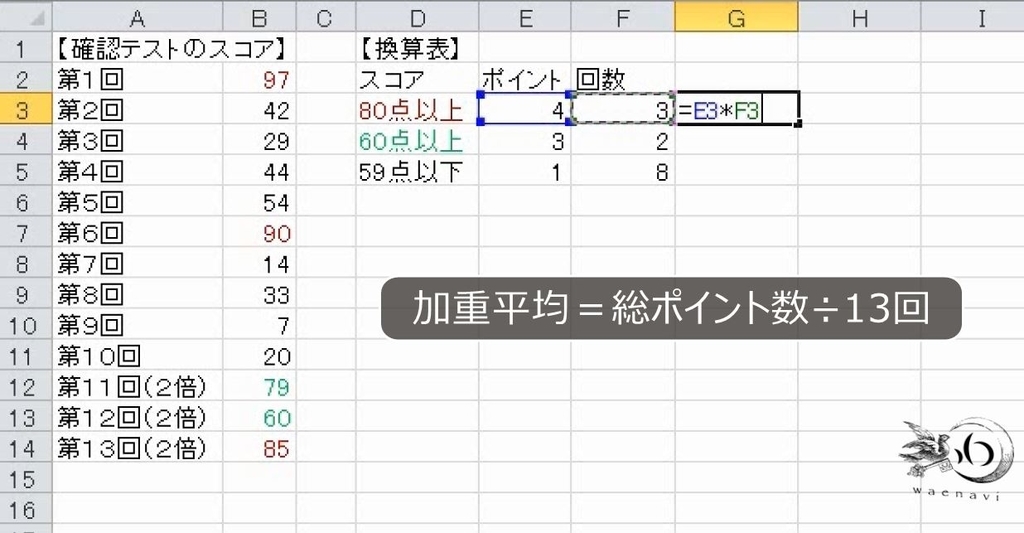
設問(1)
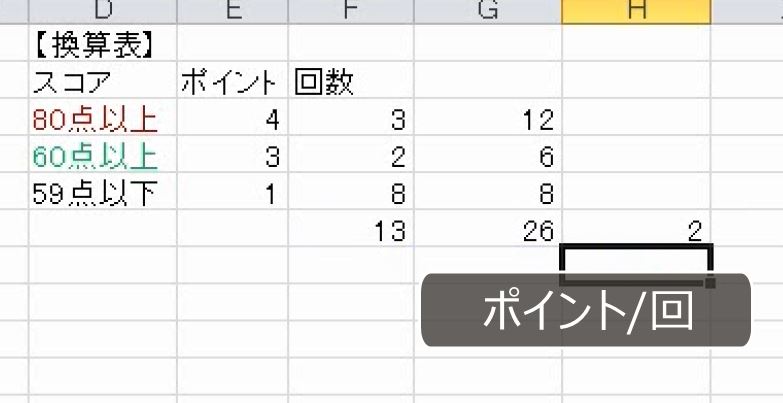
それぞれのスコアからポイントにします。このポイントを数えます。4ポイントが3回、3ポイントが2回、1ポイントが8回です。加重平均を求めます。掛け算をします。
回数とポイント数の合計を求めます。13回のテストで26ポイントです。
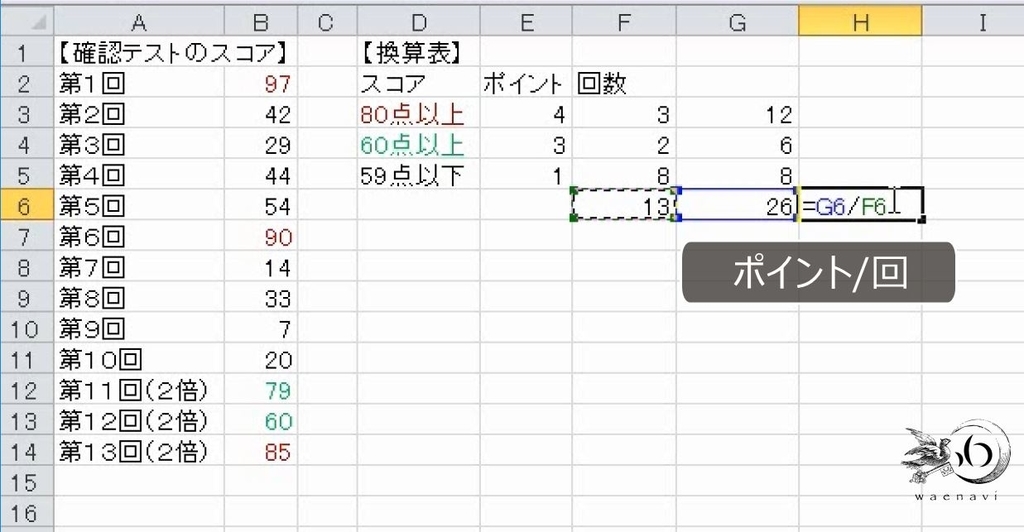
平均は2ポイントです。
設問(2)
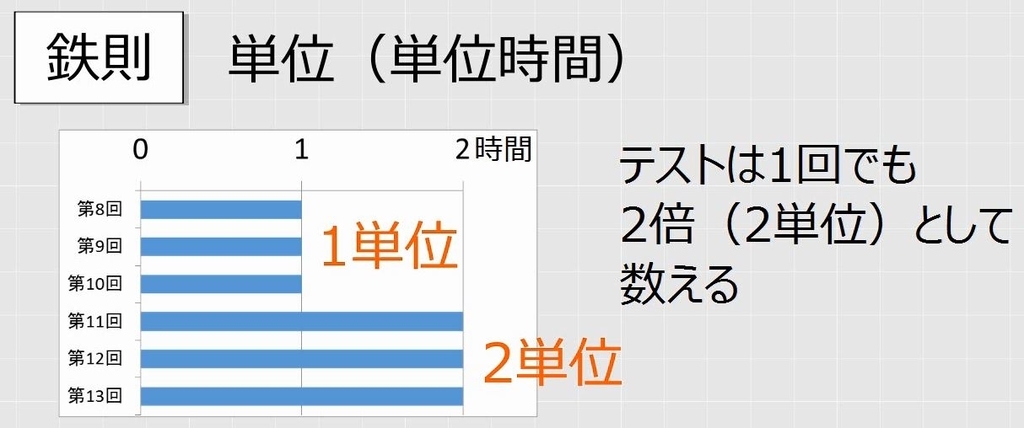
時間数や分量が2倍になると、これを2回分としてカウントすることがあり、これを1単位、2単位、・・・と数えることがあります。テストは1回であっても、その重要度から2回分のテストを受けたものとしてカウントします。
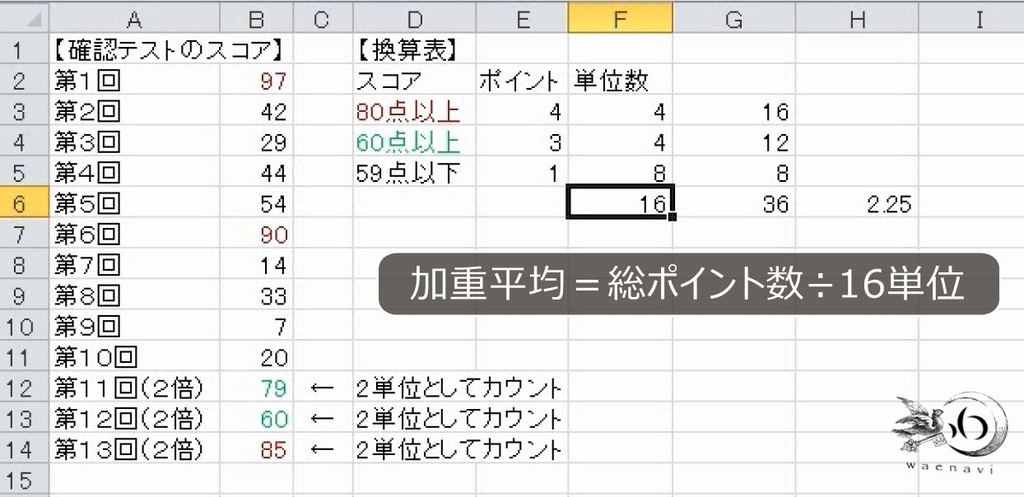
11回から13回を2単位としてカウントすると、4ポイントが4単位、3ポイントが4単位、1ポイントが8単位になります。
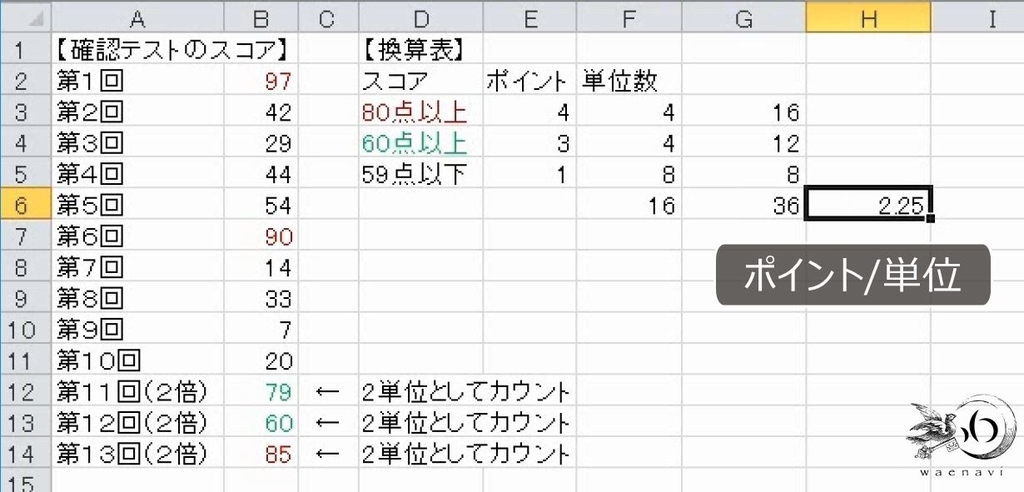
16単位で26ポイントなので、1単位当たりの加重平均は2.25ポイントになります。
8.SUMをSUMでわる
問題
各小学校の平均身長と生徒数が次の表のとおりであるとき、4つの小学校を合わせたときの平均身長を求めなさい。
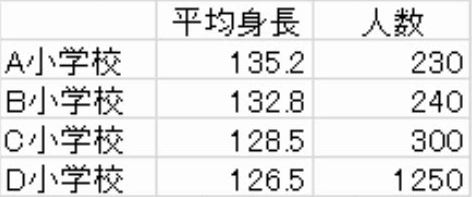
解説
平均から平均を求めるときは必ず加重平均です。いったん平均から合計を求めて、それを割り算することで平均を求めます。

各学校の平均身長に人数をかけます。これで各学校の身長の合計になります。
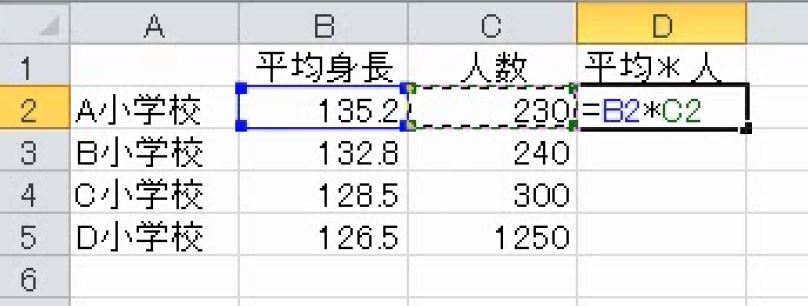
4つの合計を出します(オートSUM)。
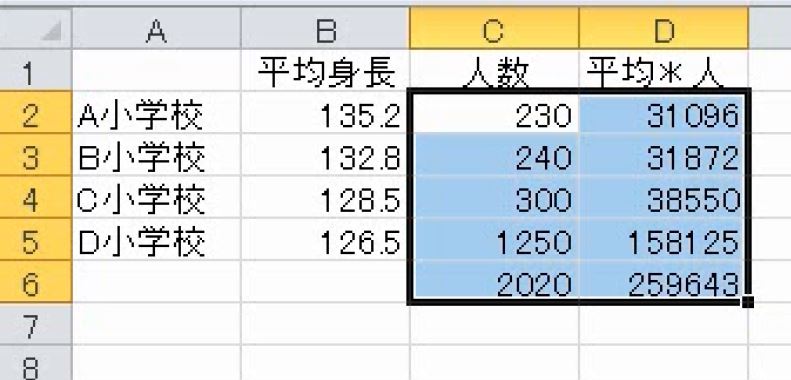
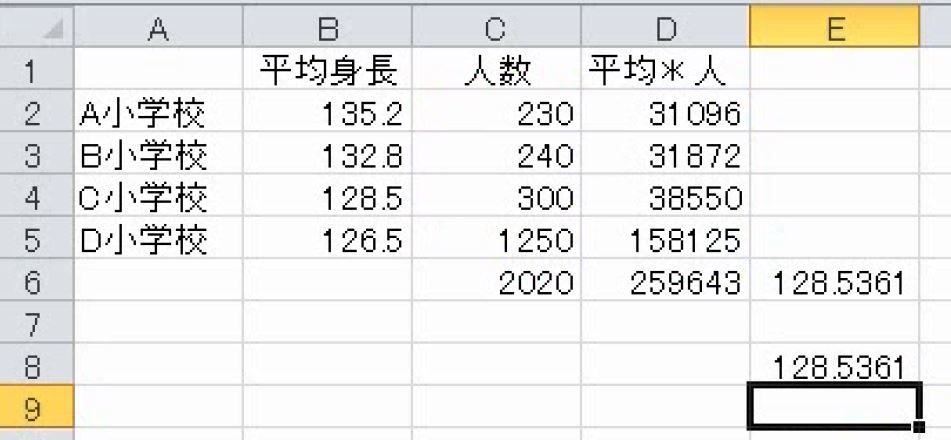
これで合計を合計で割ります。
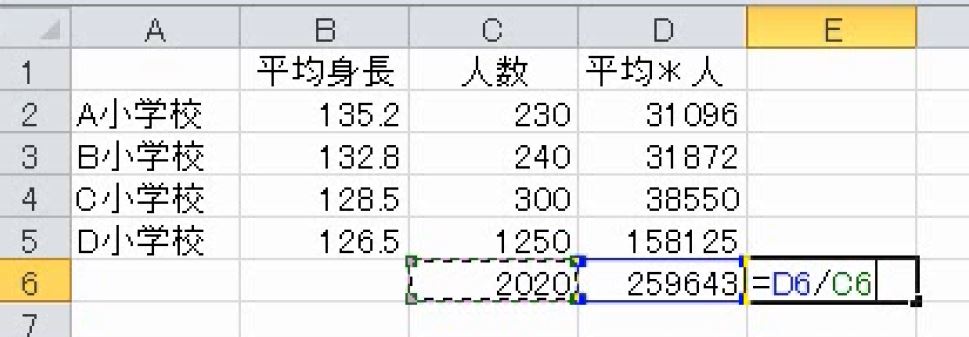
これで完成です。
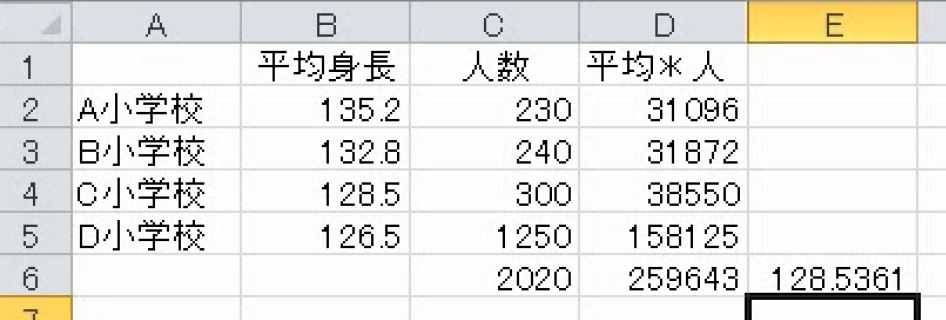
この割り算を1つの式にすることもできます。身長の総合計を出します。
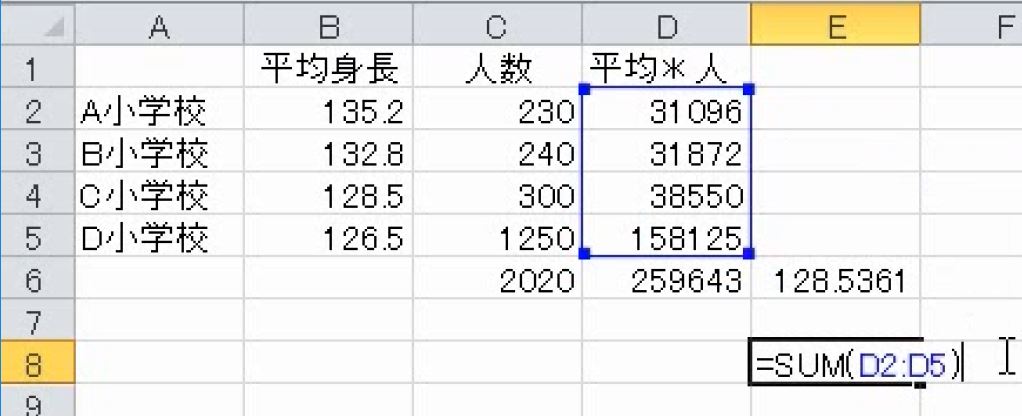
このSUMの部分をコピーします。スラッシュを入力した後に、貼り付けます。
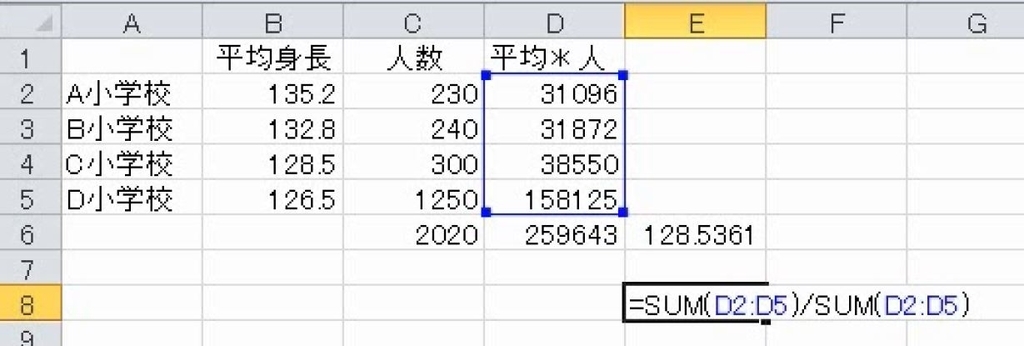
後ろの範囲をC列に直します。
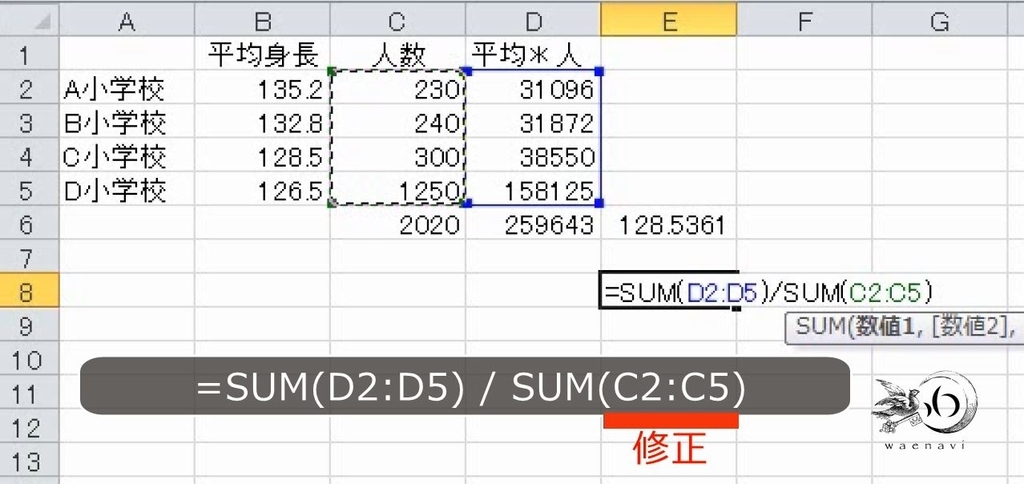
これで完成です。
9.移動平均について
加重平均と移動平均は全く違う概念です。詳しくはこちらの記事をご覧ください。
解説は以上です。
10.動画版はこちら(無料)
この記事は、わえなび実力養成講座「Excel新演習3」Program 3-7、3-8、 「ファンダメンタルExcel」Program 6-9-2 の3本のYoutube動画を書き起こしたものです。
- Excel新演習3数式・計算式集中講義 3-7 加重平均の計算1(単純平均と加重平均)【わえなび】 - YouTube
- Excel新演習3数式・計算式集中講義 3-8 加重平均の計算2(加重平均事例演習)【わえなび】 - YouTube
- ファンダメンタルExcel 6-9-2 補講 SUMをSUMでわる【わえなび】 (ファンダメンタルExcel Program6 オートSUM) - YouTube



